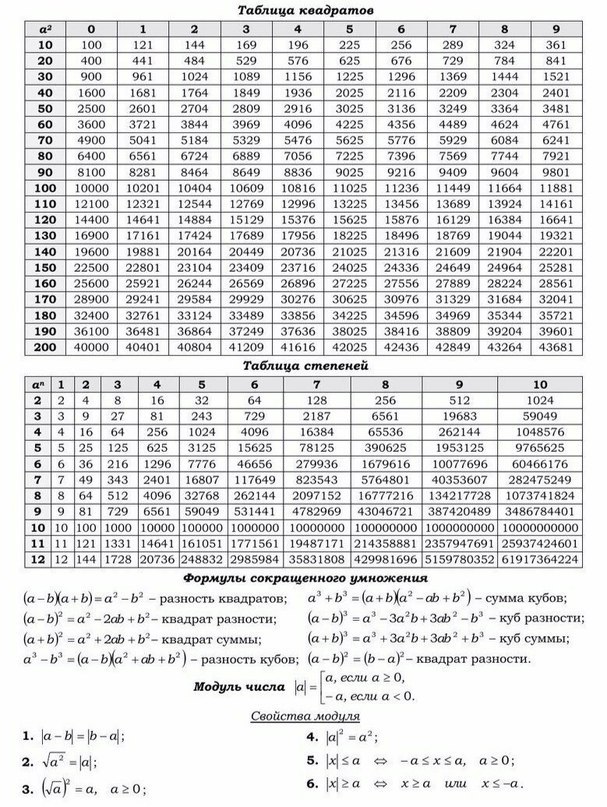
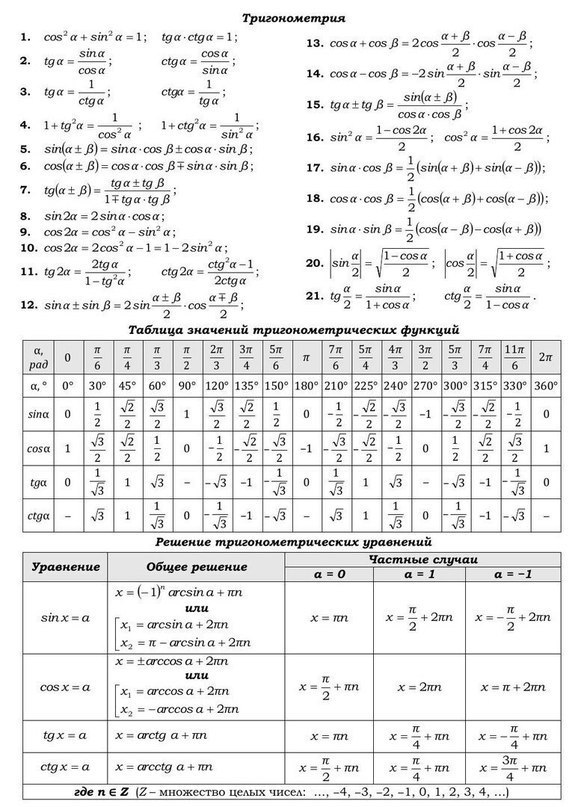
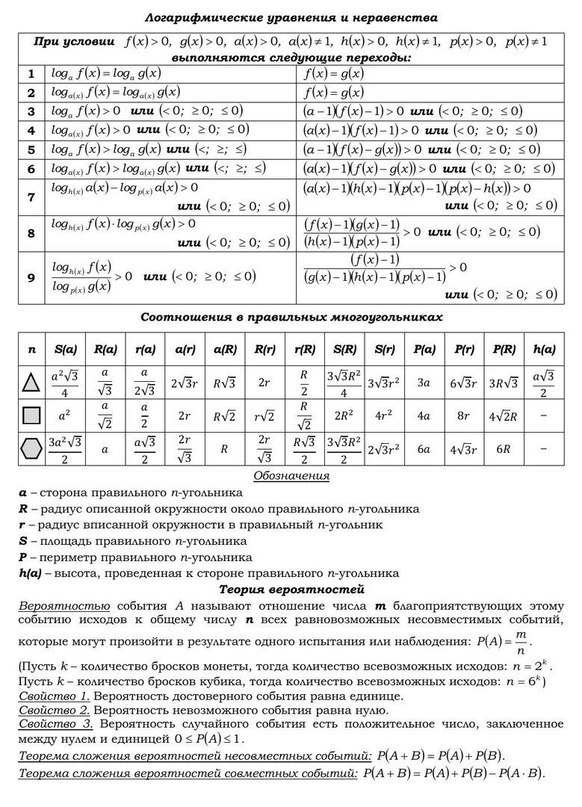
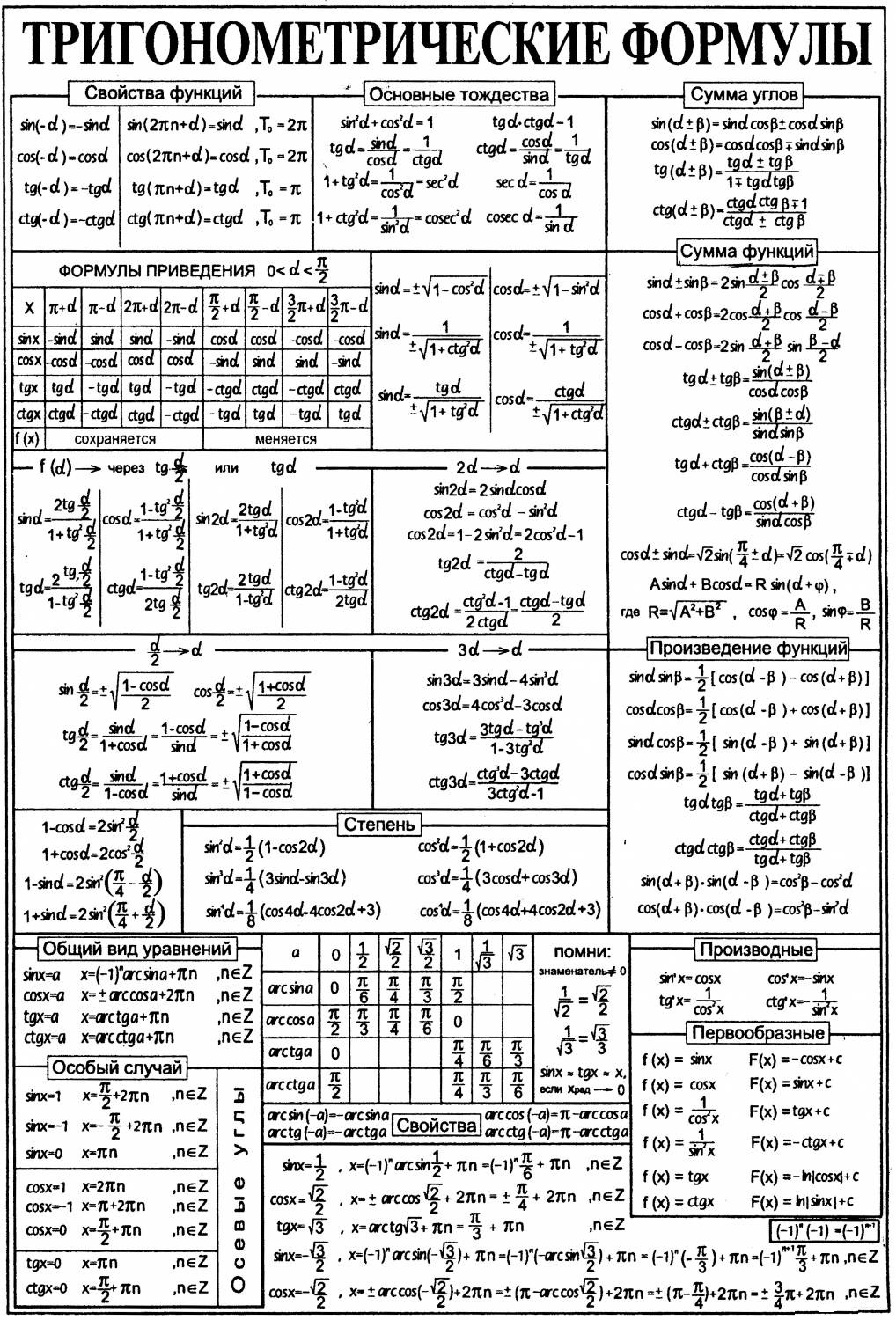
Плакаты-шпаргалки по основным предметам обучения (кликабельны!). Невозможно держать всю информацию в голове, поместите их на флешку и носите с собой.

Универсальные шпаргалки:
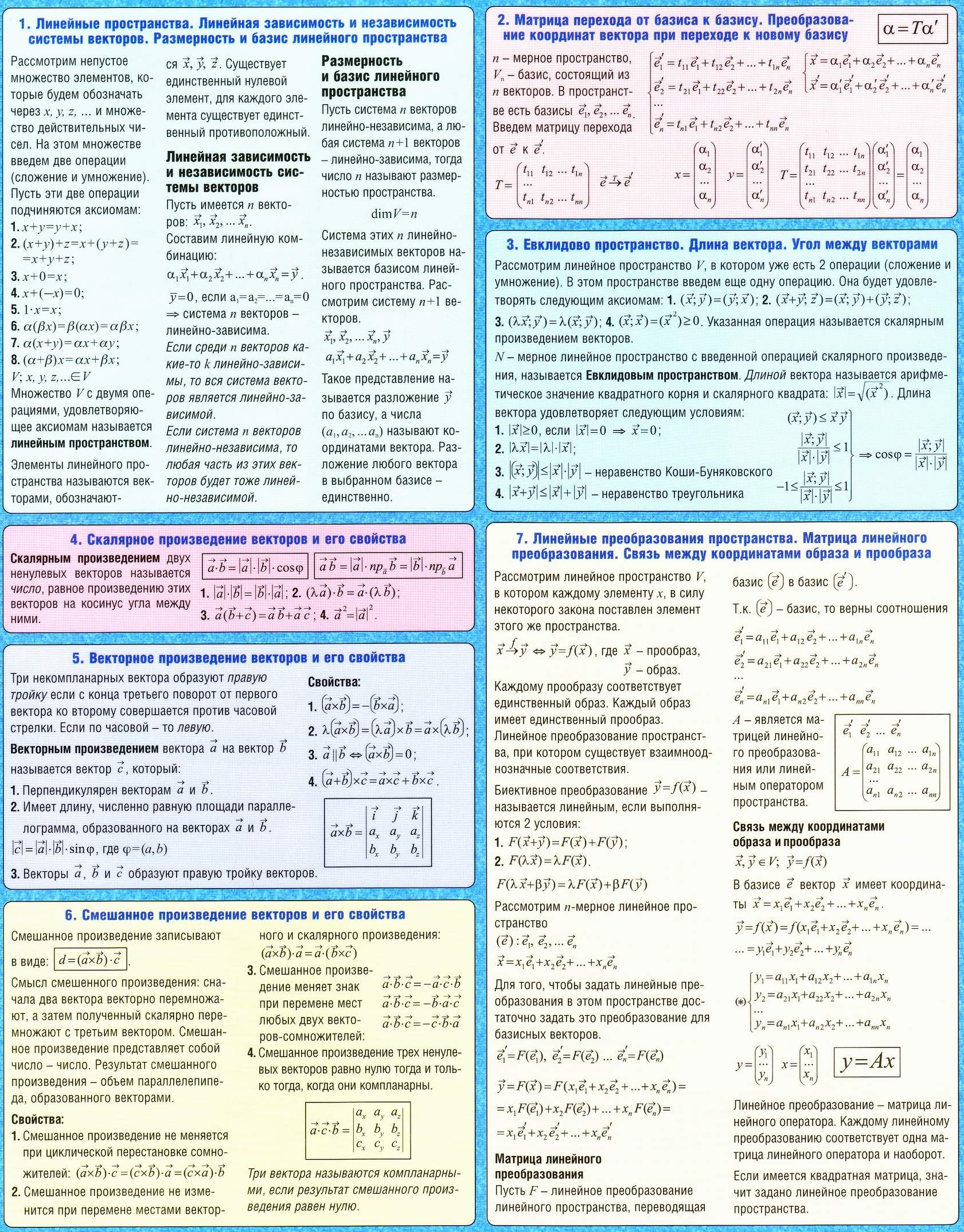
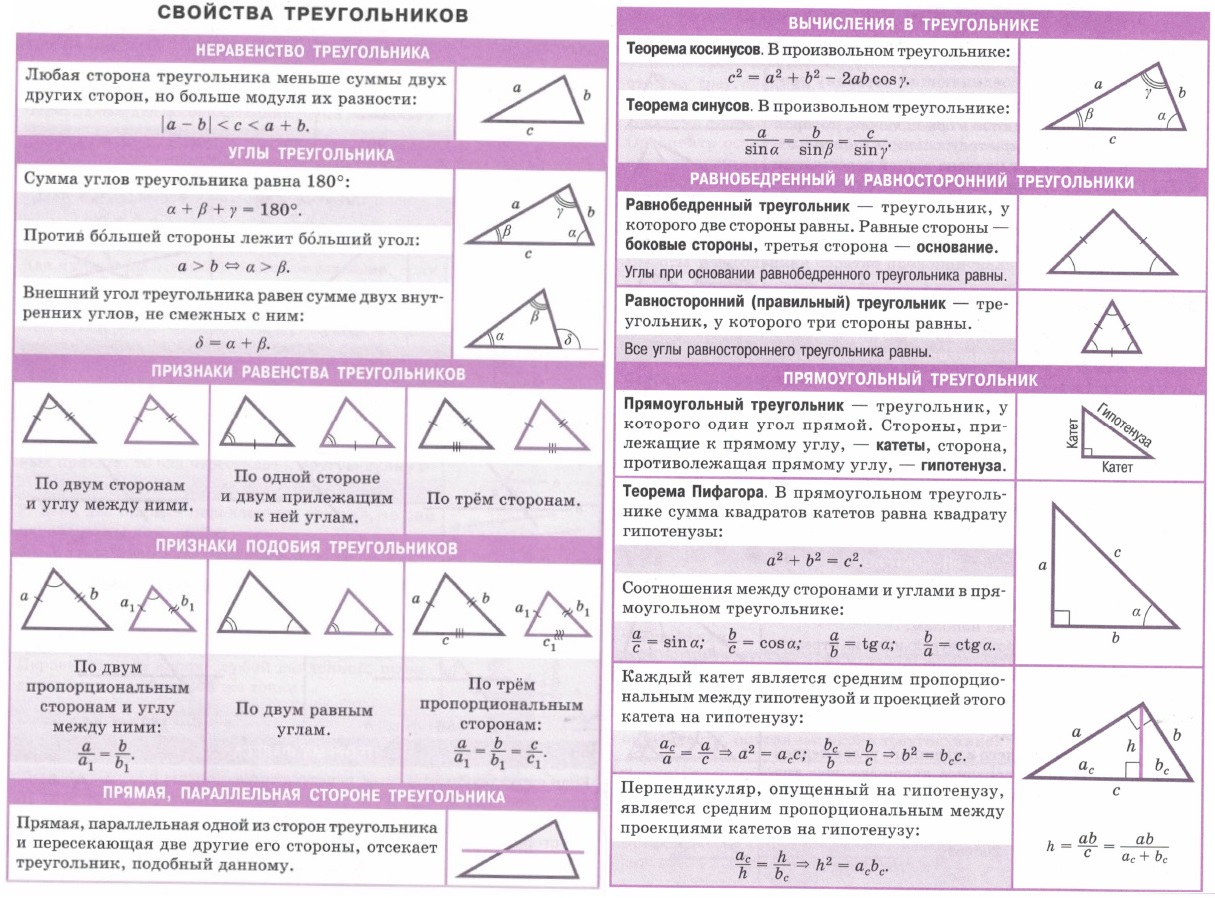
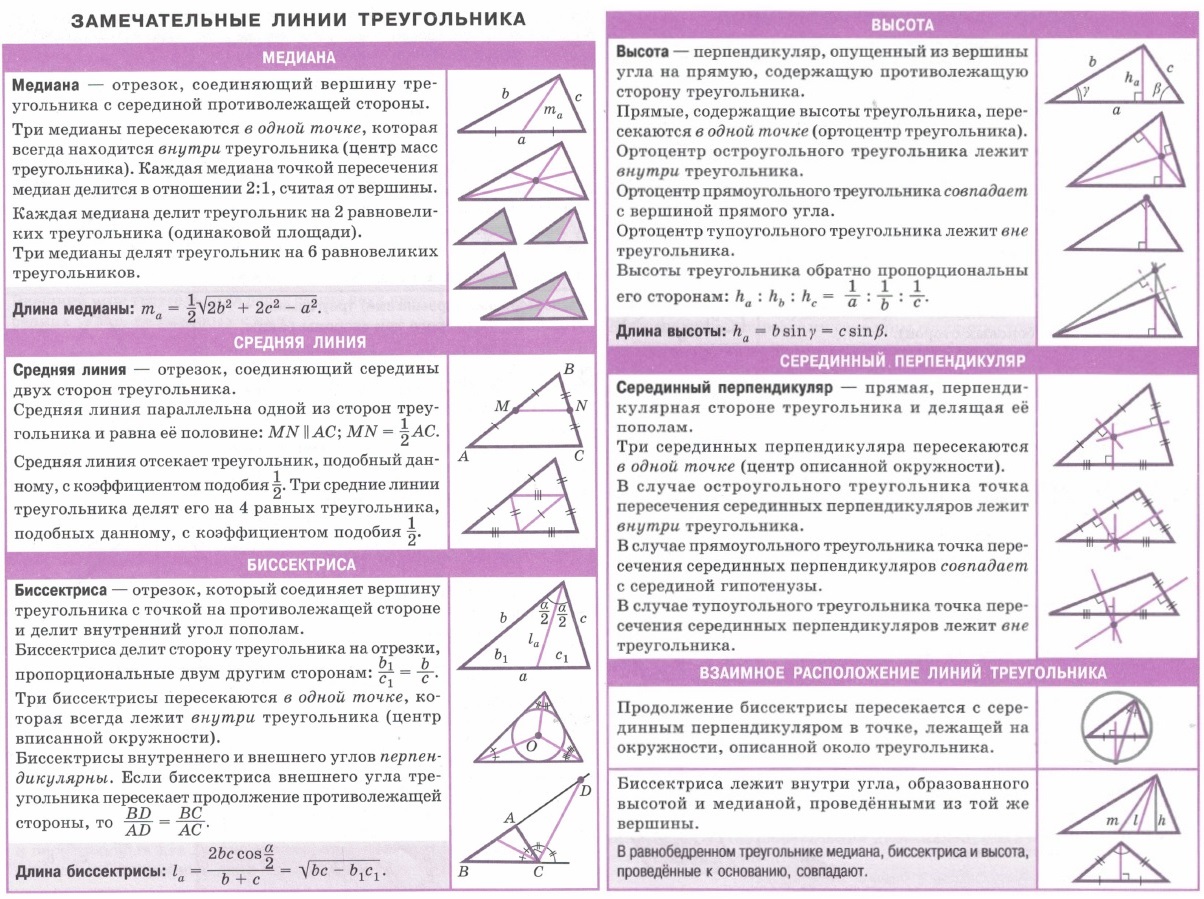
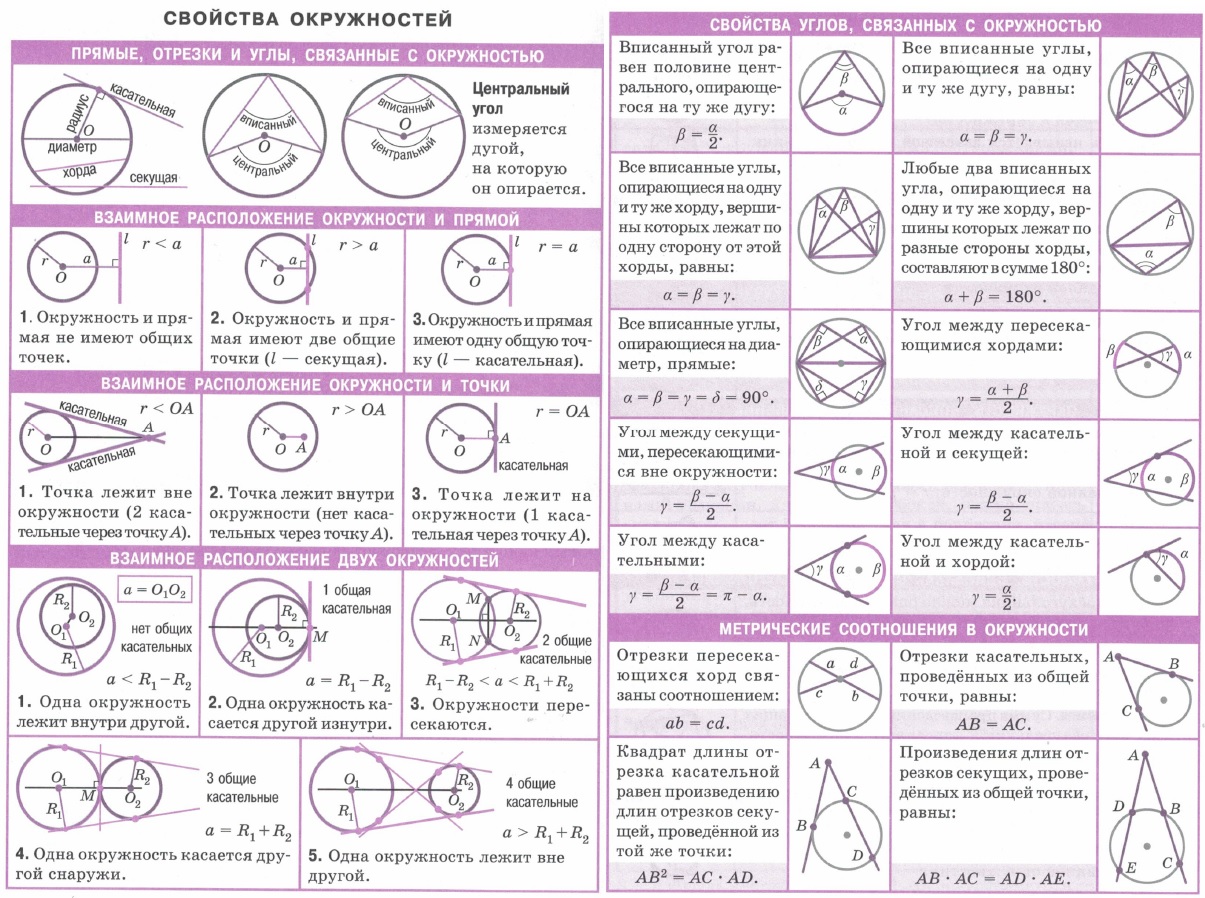
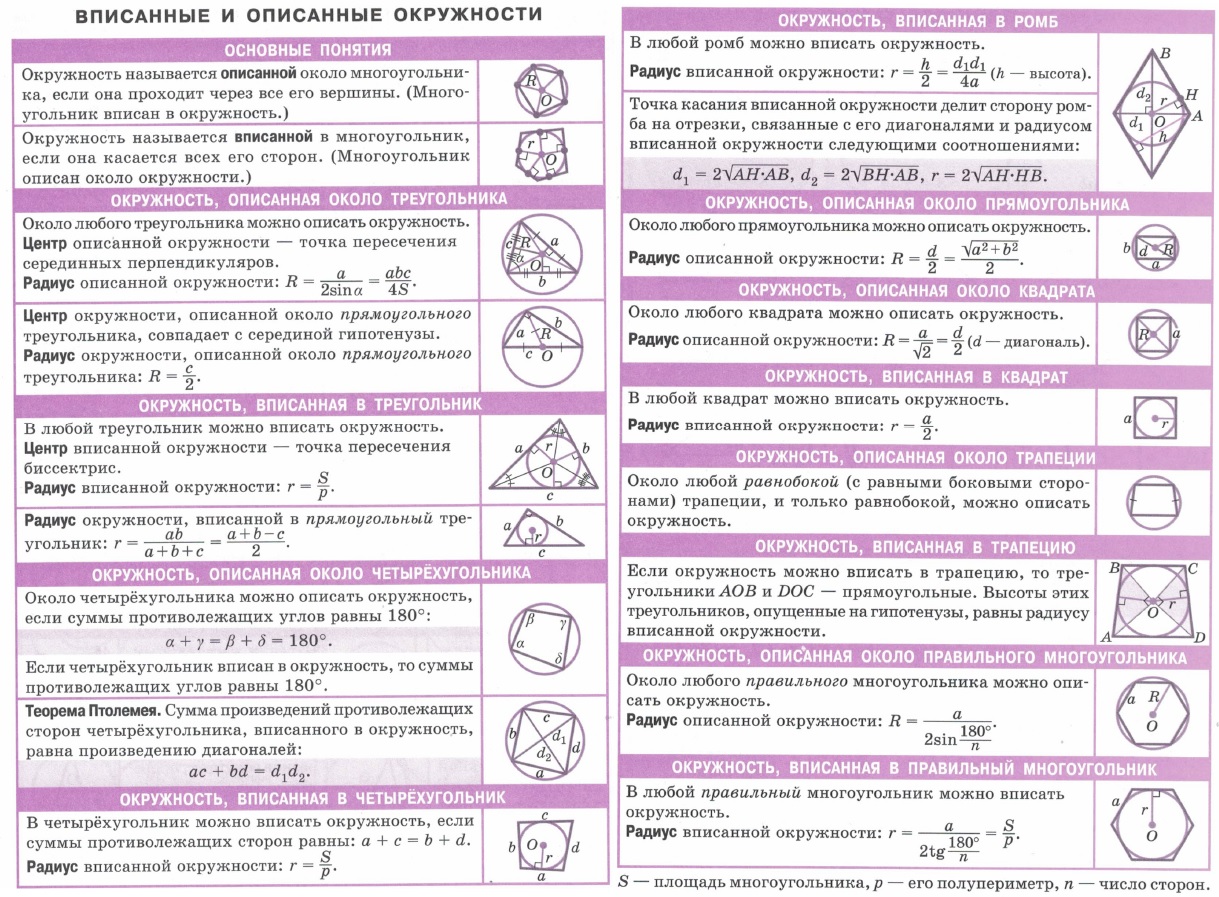
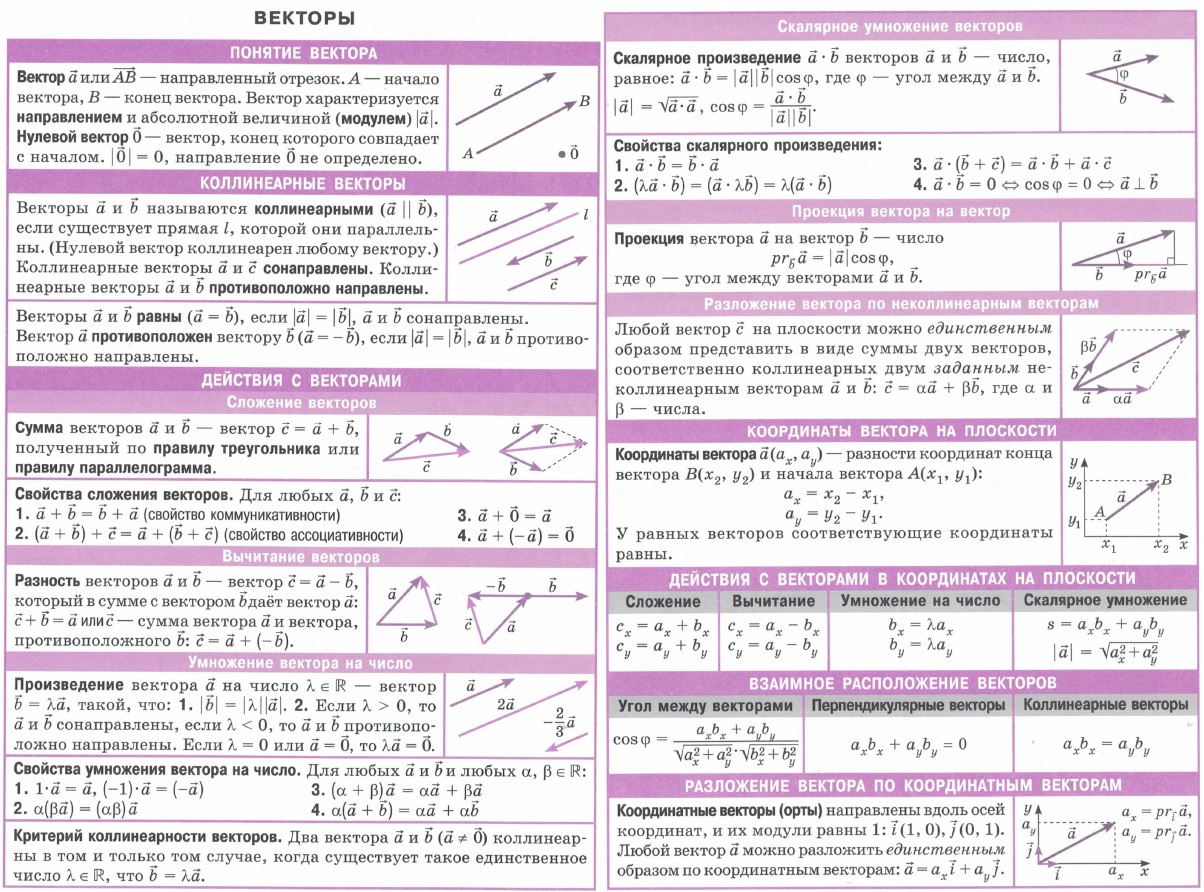
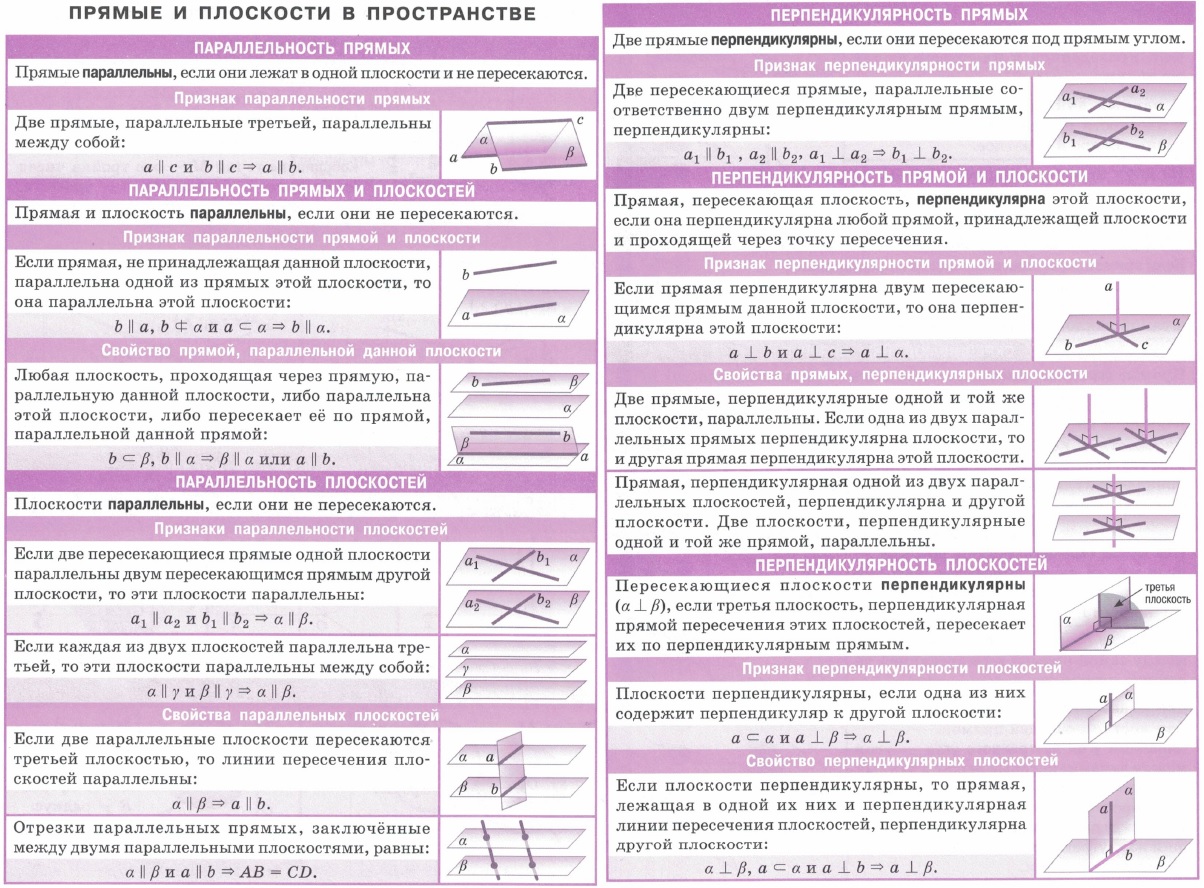
Алгебра:	Геометрия:	Русский язык:	Физика:	Химия:

http://vseshpargalki.narod.ru/Universalnye_shpargalki.html — link

Шпаргалки по математике, алгебре и геометрии

Шпаргалки по математике, алгебре и геометрии                               Шпаргалки по физике / Шпаргалки по химии Шпаргалки по математике, алгебре и геометрии Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля: Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками. Тригонометрия — основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений: Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства. Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей. Логарифмические уравнения и неравенства. Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке. Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции.             Набор 2 — Алгебра. Линейная алгебра. Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое. Тригонометрия. Основные формулы. Арксинус, арккосинус,  арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов. Графики некоторых элементарных функций.  Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона. Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при  переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. Делимость чисел. Кратное. Делитель. НОК.  НОД  Простые и составные числа. Взаимно простые числа.  Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль — свойства. Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции. Преобразование графиков функций у= f (x) в y=-f (x); y=f (-x); y=-f (-x); y=f (x-a); y=f (x)+b; y=f (ax); y=kf (x); y=|f (x)|; y=f (|x|). Построение графика обратной функции Квадратичная функция. Область определения / значений. Вершина графика функции. Нули. Свойства степеней. Св-ва арифметических корней.  Формулы сокращенного умножения. Показательная и логарифмическая функция. Область определения / значений. Промежутки знакопостоянства, монотонности, нули. Связь логарифмической и показательной функции. Свойства логарифмов. Решение показательных уравнений. Решение логарифмических уравнений. Примеры значений логарифмических и показательных функций. Тригонометрический функции синус и косинус. Область определения / значений. Промежутки знакопостоянства, монотонности, нули. Точки минимума и максимума. Четность, периоды. Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Обратные тригонометрические функции: arcsin x, arccos x, arctg x, arcctg x, графики, свойства, область определения и значений, асимптоты, промежутки знакопостоянства, возрастания, убывания. Простейшие тригонометрические функции — связь с обратными. Примеры значений обратных тригонометрических функций.  Комбинаторика. Факториал. Перестановки. Размещения. Сочетания. Биноминальные коэффициенты. Треугольник Паскаля. Свойства биноминальных коэффициентов. Формула бинома Неравенства, понятия, строгие, нестрогие, решение. Свойства неравенств. Решение линейных неравенств. Решение квадратных неравенств. Метод интервалов при решении неравенств. Решение показательных неравенств. Решение логарифмическмх неравенств. Решение иррациональных неравенств. Решение неравенств с модулем. Часто применяемые неравенства Решение тригонометрических неравенств: sin x > a, sin x< a, sin x ≥ a, sin x ≤ a; cos x > a, cos x< a, cos x ≥ a, cos x ≤ a; tg x > a, tg x< a, tg x ≥ a, tg x≤a;  ctg x > a, ctg x< a, ctg x ≥ a, ctg x≤a Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений с двумя неизвестными. Основные методы решения систем уравнений Производная функции. Определение, вторая производная, дифференцирование, геометрический и физический смысл производной, правила дифференцирования, производная сложной функции, достаточное условие монотонности функции, необходимое и достаточное условия экстремума, производные элементарных функций. Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства и геометрический смысл определенного интеграла. Физический смысл определенного интеграла Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при  переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. Набор 3 — Геометрия. Свойства треугольников, свойства четырехугольников, свойства окружностей, правильные многоугольники. Прямоугольная декартова система координат. Тела вращения. Цилиндр, конус, усеченный конус, сфера и шар, части шара. Призма. Пирамида. Различные виды углов. Построение плоских фигур. Радиальное измерение угловых величин. Свойства треугольников и правильных многоугольников. Выпуклые многоугольники. Подобие. Признаки подобия треугольников. Эллипс. Гипербола и ее свойства. Парабола и ее свойства. Полярная система координат. Цилиндрическая и сферическая системы координат. Двугранный угол. Трехгранный угол. Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции Геометрические места точек. Понятия. Примеры. Преобразования фигур. Параллельный перенос. Поворот. Преобразования симметрии относительно точки и прямой. Гомотетия. Подобие. Прямые и углы. Свойства прямых. Взаимное расположение прямых на плоскости. Аксиома параллельности и свойства параллельных прямых. Перпендикуляр и наклонные. Виды углов, свойства углов, признаки параллельности прямых, Теорема Фалеса. Свойства треугольников. Неравенство треугольника. Углы треугольника. Признаки подобия треугольников, прямая — параллельная стороне. Вычисления в треугольнике. Равнобедренный, равносторонний и прямоугольный треугольники. Замечательные линии треугольника. Медиана, средняя линия, биссектриса, высота, серединный перпендикуляр, взаимное расположение линий треугольника. Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности. Вписанные и описанные окружности. Описанные и вписанные в треугольник, четырехугольник, ромб, прямоугольник, квадрат, трапецию и правильный многоугольник окружности. Понятие вектора. Коллинеарные векторы. Действия с векторами и их свойства — сложение и вычитание векторов, умножение вектора на число, критерий коллинеарности. Скалярное умножение (произведение) векторов. Проекция вектора на вектор. Разложение векторов по неколлинеарным векторам. Координаты вектора на плоскости. Действия с векторами в координатах на плоскости. Взаимное расположение векторов. Разложение вектора по координатным векторам. Декартовы координаты на плоскости и в пространстве. Координаты точки. Координаты середины отрезка. Расстояние между точками. Уравнение прямой, уравнение плоскости. Уравнение окружности. Уравнение сферы. Прямые и плоскости в пространстве. Параллельность и перпендикулярность прямых и плоскостей. Признаки параллельности прямых и плоскостей. Признаки и свойства прямых перпендикулярных плоскости и перпендикулярных плоскостей. Перпендикуляр и наклонные. Проекция наклонной, теорема о трех перпендикулярах. Определения и признаки скрещивающихся прямых. Углы в стереометрии (плоские углы в стереометрии) Уравнения прямой на плоскости. Общее уравнение прямой. Уравнение прямой «в отрезках». Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых, проходящих через точку. Уравнение прямой, проходящей через 2 точки. Нормальное уранение прямой.

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Русский язык:
Общие сведения о русском языке	Русский язык.	Общие сведения о русском языке. Русский язык — это язык русской нации, язык, на котором создавалась и создаётся её культура.
Фонетика	Русский язык.	Фонетика — это раздел языкознания, который изучает звуковую сторону языка, т.е. способы образования и изменения звуков в речи, а также их акустические свойства.
Орфоэпия	Русский язык.	Орфоэпия — раздел языкознания, который занимается изучением нормативного литературного произношения.
Лексика	Русский язык.	Лексика — это раздел языкознания, который занимается изучением лексики (словарный состав слова).
Фразеология	Русский язык.	Фразеология — это раздел лексикологии, который изучает фразеологизмы, т.е. сложные по составу языковые единицы, имеющие устойчивый характер.
Морфемика и словообразование	Русский язык.	Морфемика и словообразование — это раздел языкознания, который изучает типы и структуры морфем, их отношения друг другу и к слову в целом.
Морфология	Русский язык.	Морфология — это раздел грамматики, который изучает разные аспекты слова: его принадлежность к определенной части речи, структуру, формы изменения, способы выражения грамматических значениях.
Синтаксис	Русский язык.	Синтаксис — это раздел грамматики, который изучает строй связной речи. Основные единицы, которые изучает синтаксис: словосочетание, предложение.
Речь	Русский язык.	Речь — это конкретное говорение, имеющее определенные временные рамки и звуковую или письменную форму.
Графика, буква, алфавит	Русский язык.	Графика, буква, алфавит — это это раздел языкознания, который устанавливает состав начертаний, употребляемых при письме, изучает соотношение между буквами и звуками.
Орфография	Русский язык.	Орфография — это система правил правописания. Основные разделы орфографии: написание морфем в различных частях речи, слитное, раздельное и дефисное написание слов, употребление прописных и строчных букв, перенос слов.
Пунктуация	Русский язык.	Пунктуация — это собрание правил расстановки знаков препинания, а также сама система знаков препинания.

Шпаргалки (шпора) по Литературе.

Литература:
Особенности жанра баллады в творчестве В. А. Жуковского	Литература.	В. А. Жуковский познакомил русского читателя с одним из наиболее любимых жанров западноевропейских романтиков — балладой.
Тема судьбы и рока в произведениях В. А. Жуковского	Литература.	Василий Андреевич Жуковский является одним из первых русских романтиков. Его по праву считают отцом русского романтизма. Белинский писал о нем: «Истинная заслуга Жуковского состоит в том, что он ввел в русскую поэзию романтизм».
Московское дворянство в изображении А. С. Пушкина и А. С. Грибоедова	Литература.	Сравнивая дворянское общество Москвы у Пушкина и Грибоедова, мне хотелось бы начать с творчества второго и не только потому, что Грибоедов писал несколько раньше, чем Пушкин, а потому, что Грибоедов свою комедию «Горе от ума» полностью посвятил дворянству Москвы.
Чацкий — комический или трагический герой?	Литература.	Грибоедов сказал: «В моей комедии 25 глупцов на одного здравомыслящего человека». С момента появления главного героя завязался его конфликт с этими 25 глупцами.
Роль любовной драмы Чацкого в основном конфликте комедии А. С. Грибоедова «Горе от ума»	Литература.	«Горе от ума» — это единственное широко известное произведение А. С. Грибоедова. Эта комедия была написана в первой четверти девятнадцатого века.
Женские образы в комедии А. С. Грибоедова «Горе от ума»	Литература.	В комедии Александра Сергеевича Грибоедова «Горе от ума» женские образы занимают особое место.
Образ Софьи — первый в русской литературе образ думающей и чувствующей женщины	Литература.	Еще В. Г. Белинский почувствовал в Софье «какую-то энергию характера» и удивился тому, что она, «не дорожа ничьим мнением», ведет себя «не по расчету, а напротив, уж слишком по нерасчету».
«Кто разгадает вас!» (Загадка Софьи в комедии А. С. Грибоедова «Горе от ума».)	Литература.	Одним из действующих лиц комедии, вызывающих и по сей день споры литераторов и критиков, безусловно, является Софья Павловна Фамусова.
"Грех не беда, молва не хороша.» (Нравственный облик «фамусовской Москвы» в комедии «Горе от ума»)	Литература.	А. С. Грибоедов в комедии «Горе от ума» очень ярко изобразил жизнь России после Отечественной войны 1812 года. Он вывел на сцену целую толпу обитателей дворянской Москвы.
«Век нынешний» и «век минувший» в комедии А. С. Грибоедова «Горе от ума»	Литература.	Комедия А. С. Грибоедова «Горе от ума» с поразительной точностью отразила основной конфликт эпохи — столкновение консервативных сил общества с новыми людьми и новыми веяниями.
Мой Пушкин	Литература.	Мне отрадно думать, что в каждом истинном читателе живет свой Пушкин... Значит, тысячи Пушкиных существуют на земле вот уже полтора века и каждый год рождаются сотни новых Пушкиных — ведь человек неповторим.
Тема поэта и поэзии в лирике А. С. Пушкина	Литература.	Эта традиционная тема волновала таких поэтов, как Гораций, Байрон, Жуковский, Державин и другие. И вслед за ними Пушкин дает свое понимание предназначения поэта и поэзии.
«Хочу воспеть Свободу миру...»	Литература.	«...Минута, и стихи свободно потекут.» Обратите внимание — «свободно»! Это ключевой слово. Даже если взять и отделить звук от смысла, сама мелодия пушкинского стиха будет звучать, как гимн Свободе.
Вольнолюбивая лирика А. С. Пушкина	Литература.	А. С. Пушкин — великий русский национальный поэт, основоположник реализма в русской литературе и русского литературного языка. В своем творчестве он уделял большое внимание теме свободы.
Философская лирика А. С. Пушкина	Литература.	А. С. Пушкин — величайший русский поэт и прозаик прошлого века. Он является основоположником новой русской литературы, одним из первых реалистов в нашей литературе.
Автор, рассказчик и герой в повести Пушкина «Капитанская дочка»	Литература.	«Капитанская дочка» — исторический роман, написанный в форме мемуаров. В этом романе автор нарисовал картину стихийного крестьянского бунта. Почему Пушкин обращается к истории Пугачевского восстания?
Проблема чести и долга в романе А. С. Пушкина «Капитанская дочка»	Литература.	Одним из самых талантливых мастеров слова XIX века является А. С. Пушкин. Он написал большое количество величайших произведений, которые навеки вошли в историю как русской, так и мировой литературы.
Человек и среда в «Евгении Онегине»	Литература.	Роман «Евгений Онегин» — величайшее создание А. С. Пушкина и при этом уникальное, не имеющее аналогий по жанру в русской и мировой литературе.
Лирическое и эпическое в романе «Евгений Онегин»	Литература.	В открывающем роман посвящении П. А. Плетневу Пушкин писал, что его произведение — это плод «ума холодных наблюдений и сердца горестных замет». Пушкин наблюдал жизнь на протяжении семи с лишним лет — с 1823 по 1830 год.
Евгений Онегин — тип «лишнего человека»	Литература.	Роман «Евгений Онегин», написанный А. С. Пушкиным в 1823 — 1831 гг., стал поистине первым подлинно реалистическим произведением. В нем автор достоверно изобразил современную ему действительность, воссоздал в образе Евгения Онегина типичный образ молодого человека 20-х годов XIX века.
Особенности композиции романа А. С. Пушкина «Евгений Онегин»	Литература.	«Евгений Онегин» лиро-эпическое произведение, в котором лирическое и эпическое переплетаются и взаимодействуют между собой на протяжении всего действия романа, при этом оба начала остаются равноправными.
«Мцыри» как романтическая поэма	Литература.	Среди русских поэтов Лермонтов занимает особое место. Поэтический мир Лермонтова — стихия мощного человеческого духа, отвергающего пошлую мелочность повседневности.
Образ России в лирике М. Лермонтова и А. Блока	Литература.	В эпоху николаевской реакции важным вопросом, волновавшим умы русской интеллигенции, был вопрос о судьбе России, о русском национальном характере.
Повести «Бэла» и «Тамань» в раскрытии образа Печорина	Литература.	Творчество Михаила Юрьевича Лермонтова формировалось в период жестокой реакции, наступившей после провала выступления декабристов. Лермонтов — это представитель светской молодежи 30-х годов XIX века.
В чем трагедия Печорина?	Литература.	Личность Печорина неоднозначна и может восприниматься с разных точек зрения. Но в любом случае нельзя отрицать трагичность данного образа. Печорин — человек, раздираемый противоречиями, предающийся постоянному самоанализу, не понятый окружающими и не понимающий их.
Печорин и Грушницкий в романе М. Ю. Лермонтова «Герой нашего времени»	Литература.	Противостояние Печорина и Грушницкого показано в главе «Княжна Мери». Повесть ведется от лица Печорина. Он склонен к анализу ситуаций, людей и самого себя, поэтому его рассказ в большей или меньшей степени можно считать объективным.
Социально-историческое и общечеловеческое в произведениях Н. В. Гоголя	Литература.	Произведения Гоголя охватывают период 40-х годов XIX века. Это время разгула бюрократии и чиновничьего аппарата в благоприятных для этого условиях русской действительности.
"На зеркало неча пенять, коли рожа крива.» (Эпиграф и сюжет комедии Н. В. Гоголя «Ревизор».)	Литература.	Эпиграф появился не сразу, а через шесть лет после выхода комедии в свет. Он стал ответом Гоголя многочисленным критикам, которые буквально обрушились и на саму пьесу, и на ее автора. Вероятно, они узнали в героях комедии себя.
Почему чиновники приняли Хлестакова за ревизора?	Литература.	«Я пригласил вас, господа, чтобы сообщить вам пренеприятное известие. К нам едет ревизор», — с этой фразы начинается блистательная комедия Н. В. Гоголя «Ревизор».
Человеческие типы в комедии Н. В. Гоголя «Ревизор»	Литература.	Когда комедия «Ревизор» вышла в свет, критики с невероятной злостью накинулись на ее автора. Гоголя обвиняли в грязной клевете на Россию, в том, что он создал «ряд смешных карикатур». Критики старались доказать, что Гоголь превратил частный случай в закономерную для России историю.
Смысл названия пьесы А. Н. Островского «Гроза»	Литература.	«Гроза» — одно из ярчайших произведений А. Н. Островского. Оно было написано в 1859 году, во время коренных перемен, происходивших в русском обществе. И не случайно Островский избрал именно такое название для своей пьесы.
Проблема поколений в романе И. С. Тургенева «Отцы и дети»	Литература.	Приступая к работе над романом «Отцы и дети», Тургенев ставил перед собой задачу проститься со старой, уходящей эпохой и встретить эпоху новую, пока еще находящуюся в поисках и метаниях. Роман «Отцы и дети» — это спор двух культур: старой, дворянской, и новой, демократической.
Проблема нигилизма в романе И.С. Тургенева «Отцы и дети»	Литература.	Основной конфликт между героем-демо кратом и либералами сформулирован в ело вах Базарова, обращенных к Аркадию Кирса нову: «Вы, например, не деретесь — и у воображаете себя молодцами, — а мы дратьс хотим».
Аркадий и Базаров (И. С. Тургенев. «Отцы и дети»)	Литература.	После выхода в свет в 1862 году роман Тургенева «Отцы и дети» вызвал буквально шквал критических статей. Ни один из общественных лагерей не принял новое творение Тургенева.
Базаров как трагический герой (по роману И. С. Тургенева «Отцы и дети»)	Литература.	Героем эпохи 60-х годов XIX века стал разночинец-демократ, убежденный противник дворянско-крепостнического строя, материалист, человек, прошедший школу труда и лишений, самостоятельно мыслящий и независимый.
Что такое «базаровщина»	Литература.	«Он в своих произведениях обыкновенно обращал внимание на вопрос, стоявший на очереди и уже смутно начинавший волновать общество»,— так писал о Тургеневе Добролюбов, характеризуя необыкновенную способность писателя откликаться на «злобу дня».
Что такое «обломовщина»? (по роману И. А. Гончарова «Обломов»)	Литература.	Н. А. Добролюбов в своей знаменитой статье «Что такое «обломовщина»?» писал об этом явлении как о «знамении времени». С его точки зрения, Обломов — это «живой современный русский тип, отчеканенный с беспощадной строгостью и правильностью».
Человеческие типы в романе И. А. Гончарова «Обломов»	Литература.	По словам Н. А. Добролюбова, автор романа стремился «случайный образ, мелькнувший пред ним, возвести в тип, придать ему родовое и постоянное значение». Сам Гончаров писал об этом так: «...Если образы типичны, — они непременно отражают на себе — крупнее или мельче — эпоху, в которой живут».
Почему «Сон Обломова» является образным и смысловым ключом к пониманию всего романа?	Литература.	И. А. Гончаров назвал «Сон Обломова» «увертюрой» всего романа. «Сон Обломова» сперва появился в свет как «эпизод из неоконченного романа».
Как отвечает Н. Г. Чернышевский на вопрос, поставленный в заглавии романа «Что делать?»	Литература.	Умение правильно поставить вопрос так же важно, как ответить на него. Например, русская литература середины девятнадцатого века конкретно спросила «Кто виноват?» и «Что делать?» Мир устроен несправедливо: богатые и бедные, добрые и злые, счастливые и несчастные...
"Особенный человек» Рахметов в романе Н. Г. Чернышевского «Что делать?»	Литература.	Сидя в одиночной камере Алексеевского равелина Петропавловской крепости, в промежутках между допросами и голодовками Н. Г. Чернышевский написал свое программное произведение «Что делать?».
Почему мне интересно читать Н. Г. Чернышевского	Литература.	Творчество Н. Г. Чернышевского вызывает у меня противоречивые мысли. Но, взвесив все плюсы и минусы, я пришла к выводу, что читать роман «Что делать?» было интересно. Изучая Чернышевского, хочется шевелить мозгами, анализировать, отвечать самой себе на трудные вопросы.
Н. А. Некрасов о назначении поэта и поэзии	Литература.	Н. Л. Некрасова можно заслуженно назвать поэтом-революционером. Он считает, что быть поэтом — это священный жребий, долг. И долг в первую очередь гражданский. «Поэт и Гражданин».
Русский народ в изображении Н. А. Некрасова	Литература.	Подавляющее большинство стихотворений Некрасова посвящено русскому мужику. Ведь куда ни кинешь взгляд — везде страдания. Едешь ли по железной дороге — за окном незримо встают тысячи безымянных людей, положивших свои жизни на ее строительство.
Духовная красота русского человека в повести Н. С. Лескова «Очарованный странник»	Литература.	Лескова на протяжении всего творчества интересовала тема народа. Он неоднократно пытался раскрыть характер, душу русского человека. В центре его произведений всегда стоят неповторимые личности, символизирующие весь народ.
Преступление и наказание в романе Ф. М. Достоевского	Литература.	Преступление Раскольникова началось не с убийства, а закончилось не признанием в полицейской конторе. Началось оно за год до совершения убийства ростовщицы — со статьи в газете, где Раскольников изложил свою жизненную позицию.
Критика индивидуалистического бунта в романе Ф. М. Достоевского «Преступление и наказание»	Литература.	Один из пяти великих романов Ф. М. Достоевского — «Преступление и наказание» — роман о необычном преступлении. Его сюжет весьма занимателен. Мы знаем, кто является убийцей, но для Достоевского наиболее важным представляется психологическое состояние героя до и после совершения преступления, борьба, которая происходит в его душе.
Преступление Раскольникова, его причины и смысл	Литература.	Главный герой романа Родион Раскольников — необычный преступник. Свое преступление — убийство ростовщицы Алены Ивановны — он совершает под влиянием созданной им философии.
Петербург в романе Ф. М. Достоевского «Преступление и наказание»	Литература.	Жизнь столицы Достоевский рисовал как яркое, резкое и «фантастическое» воплощение всех противооечий русской жизни в целом. История преступления Родиона Роскольникова разворачивается на фоне реальной жизни Петербурга середины 60-х годов XIX века.
Как Ф. М. Достоевский открывает человека в человеке	Литература.	За Достоевским давно утвердилась слава писателя-психолога, способного заглянуть в такую глубь человеческой души, которую и сам человек в себе не подозревает или которую человек знать о себе избегает.
Сатирическая направленность сказок М. Е. Салтыкова-Щедрина	Литература.	Общеизвестен особый характер таланта Салтыкова-Щедрина: все произведения писателя — сатира, доведенная до сарказма. Но зачем же смеяться над тем, над чем плакать хочется? Издревле повелось, что смех — сильт нейшее оружие разрушения гнилого, обнаружения подлого и бессмысленного.
Эзопов язык в произведениях М. Е. Салтыкова-Щедрина	Литература.	Эзопов язык, или иносказание, — восходящая к незапамятным временам форма художественной речи. Недаром она связывается с именем Эзопа — полулегендарного создателя греческой басни, жившего, по-видимому, в шестом веке до нашей эры.
Какие качества русского народа вызывают наибольшее раздражение и гнев М. Е. Салтыкова-Щедрина?	Литература.	Русский народ всегда предстает у писателя обиженным, склоненным, порабощенным. Это видение российской действительности очень сближает Салтыкова-Щедринас Некрасовым, между ними чувствуется некое родство.
«Мысль семейная» в усадьбе Головлевых (пo роману М. Е. Салтыкова-Щедрина «Господа Головлевы»)	Литература.	Многие литераторы обращались к теме семьи. Наиболее яркий пример — Л. Толстой и его «Анна Каренина». Салтыков-Щедрин семью считал одним из главных оплотов государства.
Что делает Иудушку Головлева «вечным типом»? (по роману М. Е. Салтыкова-Щедрина «Господа Головлевы»)	Литература.	Тип пустослова (Иудушки Головлева) — художественное открытие М. Е. Салтыкова-Щедрина. До этого в русской литературе, у Гоголя, Достоевского, встречаются образы, отдаленно напоминающие Иудушку, но это лишь легкие намеки.
Выморочные» герои М. Е. Салтыкова-Щедрина	Литература.	В романе Салтыкова-Щедрина «Господа Головлевы» есть глава, названная «Выморочный». Этого «звания» автор удостоил Иудушку Головлева, и оно как нельзя больше к нему подходит.
Портретная характеристика в романе Л. Н. Толстого «Война и мир»	Литература.	Жанр романа Л. Н. Толстого «Война и мир» определяется как роман-эпопея. Действительно, данному произведению присущи особенности такого жанра: большой объем, протяженность во времени описываемых событий, множество сюжетных линий и, конечно, большое количество персонажей, изображение важных для страны исторических событий.
Нравственные искания Андрея Болконского (по роману Л. Н. Толстого «Война и мир»)	Литература.	Если внимательно проследить за тем, как складывались судьбы главных героев, можно сказать: каждый из них пережил существенную эволюцию своих взглядов на жизнь. Одним из примеров является абсолютное изменение мировоззрения князя Андрея Болконского.
Кутузов и Наполеон в романе Л. Н. Толстого «Война и мир». Смысл их противопоставления	Литература.	Победа над Наполеоном осмысляется писателем с морально-философской точки зрения как победа справедливости, человечности над злом.
Наташа Ростова и Марья Болконская в романе Л. Н. Толстого «Война и мир»	Литература.	Читая роман Л. Н. Толстого «Войнаимир», мы встречаемся с очень большим количеством персонажей. Среди них множество женщин, причем самых разных: умных и глупых, божественно красивых и не особенно привлекательных, добрых и эгоистичных и т. д.
Поиски смысла бытия в лирике Ф. И. Тютчева	Литература.	Тютчев — великий трагический поэт. Его раздумья о мире, жизни, человеке глубоки и зачастую горестны. Мотивы безысходного отчаяния, страдания и одиночества не исчерпывают всего творчества поэта, но занимают в нем значительное место.
Тема семьи в романе Л. Н. Толстого «Война и мир»	Литература.	Какой должна быть семья в понимании Толстого, мы узнаем лишь в самом конце романа. Начинается же роман с описания неудачного брака. Речь идет о князе Болконском ( и маленькой княгине.
Народ и личность в романе Л. Н. Толстого «Война и мир»	Литература.	Известно, что основой «Войны и мира» Толстой считал «мысль народную»: «Я старался писать историю народа»,— одно из знаменательных высказываний автора о своем романе. Однако Андрею Болконскому и Пьеру Безухову писатель отвел в «Войне и мире» совершенно особую роль, едва ли не главную.
Образ вишневого сада в сознании героев пьесы А. П. Чехова «Вишневый сад»	Литература.	Вишневый сад объединяет вокруг себя всех героев пьесы. Писатель соединяет персонажей разных возрастов и социальных групп, и они должны будут так или иначе решить судьбу сада, а значит, и свою судьбу.
«Вишневый сад» — пьеса о прошлом, настоящем и будущем	Литература.	«Вишневый сад» — последнее произведение Чехова. Писатель был неизлечимо болен, когда писал эту пьесу. Он сознавал, что скоро уйдет из жизни, и, наверное, поэтому вся пьеса наполнена какой-то тихой грустью и нежностью.
Герои А. П. Чехова — какие они? (по рассказам А. П. Чехова)	Литература.	Я хочу рассказать о некоторых из них: пусть это будут герои рассказов «Смерть чиновника», «Хамелеон» и «Унтер Пришибеев». В рассказе «Смерть чиновника» можно заметить явное несоответствие между сюжетом, который ведет к печальному концу, и тем, как этот сюжет рассказывается.
Как и почему Дмитрий Старцев превращается в Ионыча? (по рассказу А. П. Чехова «Ионыч»)	Литература.	Кто виноват (или что виновато) в том, что молодой, полный сил и жизненной энергии Дмитрий Старцев превратился в Ионыча? Насколько исключительна или, наоборот, обыкновенна история его жизни?
...И поединок роковой...» (тема любви в лирике Ф. И. Тютчева)	Литература.	У молодого Тютчева любовь — праздник, свет, благоухание. Она — то прибежище, где можно обрести покой. Никогда не упоминается в стихах конкретная женщина, везде просто «она» — светлый, веселый, легкий образ.
Природа — сфинкс...» (Тайны мироздания в лирике Ф. И. Тютчева.)	Литература.	Тютчевская «страна» необычна — она то залита солнечным светом, то покрыта сумраком, но всегда узнаваема, близка. Если начать вспоминать стихи Ф. И. Тютчева о природе, то, наверное, большинству людей в первую очередь придет в голову «Весенняя гроза»: «Люблю грозу в начале мая...»
Вечные темы в лирике Ф. И. Тютчева и А. А. Фета	Литература.	Когда на душе неспокойно, нет ничего лучше, чем посидеть в мягком кресле с томиком стихов в руках. Стихи помогают нам отвлечься от реальных событий, заставляют размышлять на разные темы.
Поэтический образ России в лирике А. А. Блока	Литература.	Отечество для Блока — маяк, который освещает весь его творческий путь. Если проследить этот путь от начала до конца, то можно увидеть Россию во всем ее многообразии. Блок показывает нам и старую Русь, и революционную Россию, охватывая большой период истории.
Мечты и действительность в лирике А. А. Блока	Литература.	По этой «Трилогии вочеловечения» (как называл ее автор) нетрудно проследить становление Блока как поэта, постепенный переход от мечтаний к действительности. Переход, конечно, весьма условный, но заметный.
«Женские лики» в творчестве А. А. Блока	Литература.	Творческая судьба поэта всегда была неразрывно связана с его личной жизнью. Через всю жизнь он пронес чувство безграничной любви к Л. Д. Менделеевой. Это она вдохновила его на те стихотворения, которые позже вошли в сборник «Стихи о Прекрасной Даме».
Смысл названия повести А. И. Куприна «Поединок»	Литература.	Название повести Куприна верно передает смысл разыгравшейся в ней драмы, сразу определяет внутренний конфликт, еще неизвестный читателю. То есть под поединком подразумевается не только описанная в конце повести дуэль, но и все события, происходящие с главными героями.
Сила и слабость натуры подпоручика Ромашова (по повести А. И. Куприна «Поединок»)	Литература.	Рассказ о судьбе главного героя начинается уже после того, как он отслужил в полку полтора года, поскольку кардинальные, значимые перемены стали происходить с Ромашовым не с самого начала службы. Когда он только приехал в гарнизон, его обуревали мечты о славе.
Единство цикла рассказов И. А. Бунина «Темные аллеи»	Литература.	Книгу «Темные аллеи» принято называть «энциклопедией любви». Бунин в этом цикле рассказов пытался показать отношения двоих во всем многообразии проявлений. Это была та тема, которой Бунин отдавал все свои творческие силы.
Философия любви в цикле И. А. Бунина «Темные аллеи»	Литература.	Сборник «Темные аллеи» стал воплощением многолетних размышлений писателя о любви. Он видел ее повсюду, поскольку для него это понятие было весьма широким. «Темные аллеи» — произведение многоликое, разноплановое.
«Настоящую нежность не спутаешь...» (любовь в лирике А. А. Ахматовой)	Литература.	Анна Андреевна Ахматова нашла в себе силы, чтобы уже в 22 года заставить литературную общественность обратить на себя внимание. Это была женская поэзия. Но она была сильна и прекрасна.
Основные темы и идеи лирики А. А. Ахматовой	Литература.	Какие ассоциации приходят на ум при упоминании имени Анны Андреевны Ахматовой? Любовь, страстная и трагичная, самоотверженная преданность Родине, материнское горе.
Что и как читали герои русской классики?	Литература.	Комедия Д. И. Фонвизина «Недоросль». Центральная тема произведения была озвучена недорослем Митрофаном Простаковым: «Не хочу учиться, хочу жениться!»
Образы двух столиц в русской литературе	Литература.	Оба города самобытны и не похожи один на другой. Москва — всегда кипящая, жизнелюбивая, деятельная; Петербург — сумрачный, гордый, хранящий традиции.
Юмор в романе М. А. Шолохова «Поднятая целина»	Литература.	В романе «Поднятая целина» много комических сцен. Сегодня, как известно, господствует взгляд на коллективизацию как на явление трагическое, исключающее его юмористическое осмысление.
Коллективизация и судьбы крестьян в романе М. А. Шолохова «Поднятая целина»	Литература.	Последнее пятнадцатилетие утвердило взгляд на коллективизацию как на жесточайшую национальную трагедию.
Человек в огне Гражданской войны (по произведениям русской литературы XX века)	Литература.	Гражданская война,— это всегда национальная трагедия: брат идет на брата, сын — на отца. Словом, ниспровергаются все устоявшиеся нормы человеческой жизни. Но происходит ли в огне Гражданской войны очищение, самопознание человека?

Шпаргалки (шпора) по Сочинениям.

Сочинения:
Уроки Библии (притча о блудном сыне)	Сочинения.	О чем рассказывает нам притча о блудном сыне? Младший сын не захотел заниматься тяжелой работой вместе с отцом и старшим братом. Он решил отправиться в странствие, при этом попросил отца отдать причитающуюся ему долю наследства.
Ум и находчивость народа русского («Сказание о белгородском киселе»)	Сочинения.	«Сказание о белгородском киселе» — отрывок из древнерусской летописи. Прежде чем оно попало в летопись, это сказание сохранялось в памяти людей, постепенно изменялось и дополнялось.
За правое дело (роман А.C. Пушкина «Дубровский»)	Сочинения.	Роман А. С. Пушкина «Дубровский» не оставляет равнодушным никого из читателей, и это совсем не удивительно. В этом произведении показаны проблемы взаимоотношения помещиков и крестьян, отцов и детей, а также все перипетии того сложного времени.
Жажда борьбы и свободы (стихотворение М. Ю. Лермонтова «Парус»)	Сочинения.	В своем творчестве М. Ю. Лермонтов затрагивал множество различных тем. Тема борьбы и свободы отразилась в некоторых его стихотворениях, в том числе и в стихотворении «Парус».
Образ кузнеца Вакулы (по повести Гоголя «Ночь перед Рождеством»)	Сочинения.	«Ночь перед Рождеством» — повесть, вошедшая в первый сборник повестей Н. В. Гоголя «Вечера на хуторе близ Диканьки». В них автор открыл совершенно новый мир, блещущий удивительно яркими красками.
Русь, рождающая умельцев (по сказу Н.C. Лескова «Левша»)	Сочинения.	Знаменитым произведением Лескова «Левша» зачитываются как взрослые, так и дети. Простой тульский оружейник Левша вызывает не только симпатию, но и глубочайшее восхищение.
Теплый юмор А. П. Чехова (по рассказу «Лошадиная фамилия»)	Сочинения.	Великолепный сатирик А. П. Чехов бывает в своих произведениях по-настоящему беспощадным. Особенно это касается тех случаев, когда он обличает, высмеивает отрицательные человеческие качества, например пошлость, отсутствие порядочности и благородства.
Картины нищеты и страданий людей в России (по повести «Дети подземелья»)	Сочинения.	Повесть В. Г. Короленко «Дети подземелья» показывает читателю картины бедствий и страданий людей. Повествование ведется от лица мальчика из богатой семьи. Его отец — богатый и преуспевающий судья.
Над кем смеется М. Зощенко (по рассказам «Галоша», «Встреча»)	Сочинения.	Михаил Зощенко — великий юморист, рассказы которого поражают сочным, народным языком и своеобразным юмором. Герои Зощенко смешны, но вместе с тем вызывают сочувствие и жалость.
Какой смысл автор вкладывает в слова «Кладовая солнца»? (сказка-быль М. Пришвина «Кладовая солнца»)	Сочинения.	Михаил Михайлович Пришвин все свои произведения посвятил природе. В его повестях и рассказах явления природы оживают, наделяются свойствами, присущими живому существу.
«Спешите делать добрые дела» (любовь к жизни и человеку в стихотворениях А. Я. Яшина «Орел», «Покормите птиц», «Спешите делать добрые дела»)	Сочинения.	Стихотворения А. Я. Яшина заставляют читателя задуматься о человеческой жизни и о добре, которое так важно успеть сделать вовремя. Например, стихотворение «Спешите делать добрые дела» рассказывает о том, как в детстве поэт жил вместе со своим отчимом.
Какие нравственные проблемы ставит перед читателем В.П. Астафьев? (по рассказу «Конь с розовой гривой»)	Сочинения.	Рассказ Астафьева «Конь с розовой гривой» повествует об одном эпизоде из детства мальчика. Рассказ заставляет улыбнуться над проделкой главного героя и одновременно оценить замечательный урок, который преподала бабушка своему внуку.
Учитель и ученики в рассказе Ф. Искандера «Тринадцатый подвиг Геракла»	Сочинения.	Вот уже близится к концу учебный год. За окном весна, и все школьники мыслями унеслись в заоблачные дали под названием «каникулы». Но еще не время расслабляться и предаваться лени.
Идеалы М. В. Ломоносова в «Оде на день восшествия на всероссийский престол Ея Величества государыни императрицы Елизаветы Петровны»	Сочинения.	В оде Ломоносова царица Елизавета Петровна предстает возвышенным существом. Поэт возлагает на нее огромные надежды на мир и процветание России.
Рассказ А. П. Платонова «Неизвестный цветок» (мини-рецензия)	Сочинения.	Рассказ Платонова «Неизвестный цветок» заставляет читателя всерьез задуматься о трудностях человеческой жизни, хотя, на первый взгляд, речь здесь идет об обычном цветке. Впрочем, не таком уж и обычном...
Образ летописца в драме А. С. Пушкина «Борис Годунов»	Сочинения.	Одним из самых замечательных произведений, обращенных к истории России, является драма «Борис Годунов», поражающая широтой охвата русской жизни XVII века.
Фольклорные традиции в «Песне про царя Ивана Васильевича, молодого опричника и удалого купца Калашникова»	Сочинения.	«Ой ты гой еси, царь Иван Васильевич!» — звучит под сводами боярского дома пожелание благополучия. Голос гусляра звучит удивительно громко. И полилась протяжная песня, похожая на долгую дорогу гусляра от села к селу, от города к городу.
Остап и Андрий (по повести Н. В. Гоголя «Тарас Бульба»)	Сочинения.	Остап и Андрий — родные братья, но они очень сильно отличаются друг от друга. Остап обладает твердым характером, это становится ясно уже в самом начале повести. Годы, проведенные в бурсе, закалили юношу.
Поэзия народной жизни (по рассказу И. С. Тургенева «Бирюк»)	Сочинения.	Цикл И. С. Тургенева «Записки охотника» посвящен описанию жизни простого русского народа, которое происходит от лица автора — заядлого охотника, дворянина по происхождению.
Над кем смеется Салтыков-Щедрин? (по сказкам «Повесть о том, как один мужик двух генералов прокормил», «Дикий помещик»)	Сочинения.	В своих сказках М. Е. Салтыхов-Щедрин выступал против социальной несправедливости и общественного зла в любых его проявлениях.
Образ русской женщины в поэзии Н. А. Некрасова (по поэме «Русские женщины»)	Сочинения.	Поэма «Русские женщины» поражает читателя рассказом о мужестве, благородстве и силе духа жен декабристов. Поэма написана таким языком, который вызывает в душе читателя сильнейший эмоциональный отклик.
Человек и общество в изображении А Чехова (по рассказам «Злоумышленник», «Тоска»)	Сочинения.	Чехов в своих произведениях очень большое внимание уделяет отношениям человека с окружающим миром. При этом писатель никого не осуждает, он показывает отношения между людьми такими, какие они есть на самом деле.
Анализ стихотворения В. В. Маяковского «Необычайное приключение, бывшее с Владимиром Маяковским летом на даче.»	Сочинения.	Стихотворение Маяковского «Необычайное приключение, бывшее с Владимиром Маяковским летом на даче...» — одно из удивительных творений поэта, в котором его поэтический стиль раскрывается особенно ярко.
Тема природы в творчестве Е. И. Носова (по рассказу «Кукла»)	Сочинения.	Рассказ Носова «Кукла» заставляет задуматься о нравственной чистоте человека. Старый Акимыч и его собеседник неторопливо бредут по улице. И вдруг внимание Акимыча привлекает сломанная кукла.
Тема памяти в рассказе Ю. В. Бондарева «Простите нас!»	Сочинения.	«Школьные годы чудесные», — поется в одной очень хорошей песне. Но эти «чудесные» годы быстро пролетают, иногда не оставляя в памяти бывших учеников абсолютно никакого следа.
Братья наши меньшие (по рассказу Л. Андреева «Кусака»)	Сочинения.	В рассказе Андреева «Кусака» речь одет о проблеме совести и человеческой доброты. Человек считает себя добрым и благородным, но при этом не замечает преданности братьев своих меньших, относится к ним, как к игрушке.
Гринев и Швабрин (по повести А Пушкина «Капитанская дочка»)	Сочинения.	Герои повести Пушкина Петр Гринев и Алексей Швабрин сразу же привлекают внимание читателя. С самого начала знакомства с ними выясняется, что общего у этих людей очень и очень мало.
Анализ повести И Тургенева «Первая любовь»	Сочинения.	Повесть И. С. Тургенева «Первая любовь» появилась в 1860 г. Автор особенно дорожил этим произведением, наверное, потому, что повесть эта во многом автобиографична.
Мцыри — образ сильного человека (по поэме М. Ю. Лермонтова «Мцыри»)	Сочинения.	В произведении Михаила Юрьевича Лермонтова «Мцыри» рассказывается история короткой жизни юноши, воспитанного в монастырских стенах и осмелившегося бросить вызов царящим вокруг деспотизму и несправедливости.
Что мы узнаем в сцене фантастического вранья Хлестакова о его реальной петербургской жизни?	Сочинения.	В третьем действии комедии Н. В. Гоголя «Ревизор» читатель сталкивается с неожиданным и мощным потоком вранья, исходящим из уст одного из центральных персонажей — Ивана Александровича Хлестакова.
«Ася» — повесть о любви	Сочинения.	Повесть «Ася» заставляет читателя еще раз задуматься о любви. Никто не спорит с тем, что любовь — самое прекрасное, возвышенное и благородное чувство на свете, но, к сожалению, далеко не всегда мы в состоянии понять, а действительно ли чувство, испытываемое нами, и есть любовь.
Образ Ивана Васильевича (по рассказу Л. Н. Толстого «После бала»)	Сочинения.	Размышления об образе Ивана Васильевича, от лица которого ведется повествование в рассказе Толстого «После бала», заставляют читателя в должной мере оценить душевные качества главного героя.
В чем смысл жизни? (размышления над «Песней о Соколе» М. Горького)	Сочинения.	Каждый человек в той или иной степени задумывается о смысле жизни. Обыденная реальность не может заполнить пустоты в душе, если у человека нет какой-либо значительной цели.
Мир поэзии Н. А. Заболоцкого (по стихотворению «Я воспитан природой суровой»)	Сочинения.	Стихи — это способ выражения человеком своих самых сокровенных чувств, мыслей, намерений. Каждый человек обладает бессмертной и неповторимой душой, надеждами, мечтами.
Образ Василия Теркина (по поэме А. Т. Твардовского «Василий Теркин»)	Сочинения.	Поэма «Василий Теркин» была написана Александром Трифоновичем Твардовским во время Великой Отечественной войны и публиковалась в различных газетах по главам.
Русская деревня в 30-е гг. XX в. (по рассказу В. П. Астафьева «Фотография, на которой меня нет»)	Сочинения.	Рассказ «Фотография, на которой меня нет» — отдельная глава из книги «Последний поклон», однако она воспринимается как самостоятельное произведение. В ней развивается сразу несколько тем, в том числе и тема деревенской жизни.
Что возмущает Чацкого в эпизоде с «французиком из Бордо»?	Сочинения.	Прежде чем ответить на данный вопрос, мне хотелось бы ненадолго вернуться в прошлое и посмотреть, как развивалось действие комедии до этого гневного и обличительного выступления Чацкого.
«Наука страсти нежной» и подлинная любовь в жизни Онегина	Сочинения.	В первой главе романа А. С. Пушкина «Евгений Онегин» мы знакомимся с главным героем, узнаем о его жизни — пустой и бессмысленной.
Анализ стихотворения М. Ю. Лермонтова «Родина»	Сочинения.	«Родина», по утверждению автора статьи в лермонтовской энциклопедии, является одним из самых замечательных произведений русской лирики XIX в. Написанное в последний год жизни, оно привлекло к себе внимание еще до публикации.
Анализ повести Н. В. Гоголя «Шинель»	Сочинения.	Повесть была излюбленным жанром Н. В. Гоголя. Он создал три цикла повестей, и каждый из них стал принципиально важным явлением в истории русской литературы.
Герой «Юности» Л. Н. Толстого	Сочинения.	Главный герой повести «Юность» — Николенька Иртеньев. Толстой его рисует уже взрослым, молодым человеком, у которого выработались определенные правила, мысли и взгляды на жизнь.
«За все в ответе» (по произведению Ч. Айтматова «Материнское поле»)	Сочинения.	Чингиз Айтматов — один из самых известных писателей нашего времени. Его замечательные произведения «Материнское поле», «Первый учитель», «Белый пароход» и многие другие прочно вошли в русскую литературу.
Комическое и трагическое в комедии Д. И. Фонвизина «Недоросль» (мини-рецензия)	Сочинения.	Комедия Фонвизина «Недоросль» заставляет читателя улыбнуться над смешными и нелепыми героями. Писатель высмеивает дремучее невежество и нежелание хоть как-то изменить ситуацию, неправильное воспитание дворянских детей, их лень и отсутствие собственной позиции.
Фольклорные мотивы в «Слове о полку Игореве»	Сочинения.	Уникальный памятник древнерусской литературы «Слово о полку Игореве» сочетает в своей структуре два контрастирующих стилистических элемента: книжный и фольклорный.
Романтические поэмы В. А. Жуковского («Светлана», «Людмила»)	Сочинения.	«Людмила» — первая поэма Жуковского, являющаяся великолепным образцом романтического жанра. Самое начало поэмы ясно доносит до читателя всю глубину чувств Людмилы, ожидающей своего возлюбленного.
Молчалинское в героях комедии А. С. Грибоедова	Сочинения.	В комедии «Горе от ума» А. С. Грибоедов показывает жизнь московского общества, рисует целый ряд образов, весьма характерных для того времени.
Мои любимые афоризмы в комедии «Горе от ума»	Сочинения.	Литературная критика двадцатых годов девятнадцатого века особенно хвалила ту тонкость и изящество, с какими Грибоедов «переложил в непринужденные рифмы» живой «разговорный язык».
«Все тихо, просто было в ней.» (Татьяна Ларина в авторской оценке)	Сочинения.	Образ Татьяны, созданный Пушкиным в романе «Евгений Онегин», имеет не меньшее значение, чем образ главного героя, Онегина.
«Лишь голос твой поет в моих стихах.» (тема любви в творчестве Анны Ахматовой)	Сочинения.	Поэзия Ахматовой — это особый мир, который, словно обладая магической силой, притягивает к себе снова и снова. Перечитывая ее стихи, постоянно находишь в них что-то новое, какие-то струнки, которые ранее молчали.
Проблема чести и долга (на примере литературного материала или по жизненным впечатлениям)	Сочинения.	Проблема чести и долга для многих заключается в том, что второе понятие принимается как общее, а первое — глубоко индивидуально. Бывает очень непросто выполнить долг, не запятнав свою честь в глазах окружающих.
Каким представляла Катерина Бориса, и каким он оказался?	Сочинения.	Любовь Катерины к Борису на время увеличивает границы тесного мирка, в котором до сих пор живет девушка. Катерина испытывает столь сильное чувство впервые. Девушка была выдана замуж насильно за нелюбимого человека.
Роман И. А. Гончарова «Обломов» (размышления над прочитанным)	Сочинения.	Роман Гончарова «Обломов» заставляет читателя задуматься о смысле жизни. Кто такой Илья Ильич Обломов? Обыкновенный лентяй или человек, не видящий абсолютно никакого смысла в жизни?
«Отцы» и «дети» в одноименном романе И. С. Тургенева	Сочинения.	Проблема отсутствия взаимопонимания между представителями различных поколений является древней, как мир. Уже в самом названии писатель определил главную задачу своего произведения.
Поэзия Марины Цветаевой — дневник ее души	Сочинения.	Любовь к поэзии проснулась у Цветаевой рано. Еще будучи совсем юной, она тайком от семьи выпустила свой первый поэтический сборник «Вечерний альбом». Отзывы на эту книгу были весьма благосклонными, что вселило в юную поэтессу уверенность в своих силах.
Анализ стихотворения А. Блока «Незнакомка»	Сочинения.	Это стихотворение Александра Блока принадлежит к периоду написания «Страшного мира», когда главными в восприятии поэтом мира были ощущения тоски, отчаяния и неверия.
«Моя лирика жива одной большой любовью, любовью к Родине» (тема Родины в поэзии С. Есенина)	Сочинения.	Сергей Александрович Есенин — величайший поэт начала XX в. Человек, в своих стихах восхваляющий родину, людей, природу. Его стихи, насыщенные любвеобильностью, достаточно полно характера зуют Россию.
Трагедия Мастера (по роману М. Булгакова «Мастер и Маргарита»)	Сочинения.	Слово «мастер» не случайно вынесено Булгаковым в заглавие его знаменитого романа «Мастер и Маргарита». Он действительно является одной из центральных фигур булгаковского произведения.
Путешествие в фантастический город Чевенгур (по роману А. Платонова «Чевенгур»)	Сочинения.	«Чевенгур» Андрея Платоновича Платонова — это сатира на первые послевоенные годы в России. Это роман, трагедия, хроника, социальная фантастика, исповедь о том времени, когда люди верили, «что еще рожь не поспеет, а социализм будет готов».
Мое открытие Набокова	Сочинения.	Творчество Владимира Набокова произвело на меня глубокое впечатление. Блестящий русский писатель XX в., долго не признаваемый у себя на родине, он обрел славу и почитание за границей.
Судьба народа в трагические периоды истории (по произведениям М. А. Шолохова)	Сочинения.	В творчестве Шолохова, при сохранении классических конфликтов русской литературы, показана трагедия столкновения человека с роковыми силами судьбы. Произведения этого автора охватывают более полувека истории России, истории бурной и тяжелой.
Символ целой эпохи (по повести Солженицына «Один день Ивана Денисовича»)	Сочинения.	Образ Ивана Денисовича возник на основе реального прототипа, которым стал солдат Шухов, воевавший вместе с автором в советско-германскую войну (но никогда не отбывавший наказание), а также благодаря наблюдениям за жизнью пленников и личному опыту автора, приобретенному в Особом лагере, где он работал каменщиком.
Чем мне близка поэзия В. Высоцкого?	Сочинения.	Мне очень близка поэзия Владимира Семеновича Высоцкого, к сожалению, ушедшего из жизни на пике своего творческого расцвета. Близка темами, идеями, мотивами, но больше всего—жизненной правдой.
«Все человечество любить намного проще, чем одного конкретного человека» (сочинение-рассуждение)	Сочинения.	Каждый из нас видел влюбленного человека, возможно, был на его месте: до чего счастливые у него глаза! Они сверкают, словно звезды на ночном безлунном небе... Походка становится легкой и невесомой: за спиной же выросли невидимые, к сожалению, для других крылья.
Крах надежд и ожиданий главной героини пьесы Островского «Бесприданница»	Сочинения.	В своей пьесе Островский раскрывает всю систему отношений, складывающихся между обществом и женщиной. За внешним лоском и погоней за деньгами сильные мира сего стали забывать о простых человеческих чувствах.
Базаров — предмет подражания и ненависти героев романа И. С. Тургенева	Сочинения.	В романе «Отцы и дети» воссоздана эпоха, предшествовавшая отмене крепостного права. В обстановке кризиса резко обострились споры разных поколений о народе, общественном строе, искусстве, религии.
Мотивы и образы лирики Ф. И. Тютчева	Сочинения.	В творчестве Тютчева раскрыты многие темы, которые прошли через его стихи горячими волнами любви и чувства, участия и непревзойденного дара сопереживать. Одним из мотивов его творчества является мотив родины — России.
Проблема народного счастья в поэме Некрасова «Кому на Руси жить хорошо»	Сочинения.	«Я лиру посвятил народу своему», — писал Некрасов в стихотворении «Элегия». Народная тема волновала писателя как никакая другая, поэтому он посвятил ей поэму-эпопею «Кому на Руси жить хорошо».
Сочинение Салтыкова-Щедрина «Господа Головлевы» как попытка создания «семейного» романа	Сочинения.	Критики называли Салтыкова-Щедрина «великим мастером смеха», но, читая его роман-хронику «Господа Головлевы», мы не смеемся, потому что тяжелое, гнетущее чувство пронизывает это произведение от начала и до конца.
В чем секрет актуальности романа Ф. М. Достоевского «Преступление и наказание»?	Сочинения.	Роман Ф. М. Достоевского можно назвать одним из самых сложных произведений русской классической литературы. Автор талантливо отразил потрясения и терзания главных героев, которые не могут не взволновать человека.
Женские образы в романе Ф. М. Достоевского «Преступление и наказание»	Сочинения.	Автор романа «Преступление и наказание» знакомит нас со многими человеческими судьбами, столкнувшимися с тяжелейшими условиями существования. В результате некоторые из них оказались на самом дне общества, не выдержав того, что выпало на их долю.
Смысл названия романа Л. Н. Толстого «Воскресение»	Сочинения.	Роман «Воскресение» написан Л. Н. Толстым в 1899 г., как раз в то время, когда страна была повергнута в ужас: «Переполненная Сибирь, тюрьмы, война, виселицы, нищета народа, кощунство, жадность и жестокость властей...»
Пьер Безухов и Андрей Болконский — два воплощения одного авторского идеала	Сочинения.	Роман Толстого «Война и мир» познакомил нас со многими героями, обладающими лучшими человеческими качествами, благородными, целеустремленными, добросердечными ревнивцами высоких нравственных идеалов.
Наташа Ростова — любимый женский образ автора романа «Война и мир»	Сочинения.	Идеалом женщины для Толстого является героиня романа «Война и мир» Наташа Ростова. С первых строк мы видим, насколько симпатизирует ей писатель, который старался показать свою любимую героиню в самых ярких моментах ее жизни.
Жизненные перипетии главного героя повести Н. С. Лескова «Очарованный странник»	Сочинения.	Одним из самых замечательных и значительных произведений Н. С. Лескова является повесть «Очарованный странник», в которой автор как истинный художник запечатлел замечательный тип русского мужика в образе главного героя — Ивана Северьяныча Фпягина.
Неприятие автором жизненной позиции своих героев в рассказах «Человек в футляре», «Крыжовник», «О любви»	Сочинения.	Рассказы «Человек в футляре», «Крыжовник», «О любви» задумывались Чеховым как части одного большого цикла, который, к сожалению, так и не был закончен. На принадлежность их к одной серии указывает общность идеи, мыслей и даже главных героев.
Мир новый и мир старый в пьесе А. П. Чехова «Вишневый сад»	Сочинения.	В пьесе «Вишневый сад» Чехов показал гибель дворянского класса под напором капитализма. Пьеса была очень актуальной для того времени, она отвечала на те вопросы, которые волновали русское общество в начале XX в.
Особенности бунинской прозы (по рассказам «Господин из Сан-Франциско» и «Солнечный удар»)	Сочинения.	В своих произведениях Бунин, с одной стороны, показывал картину своего времени (рабство одних, непомерное господство других), а с другой — раскрывал таинства человеческой души, обличая дурные качества внешне порядочных людей и показывая положительные — негодяев и безнадежных с точки зрения общества.
Повесть А. И. Куприна «Поединок»: сюжет и герои	Сочинения.	Повесть А. И. Куприна «Поединок» — одно из лучших произведений писателя. Основанное на автобиографических мотивах, оно воплотило в себе все впечатления автора от учебы в кадетском корпусе и четырех лет военной службы.
«Полесская сказка» А. И. Куприна (анализ повести «Олеся»)	Сочинения.	Повесть Куприна «Олеся» не может оставить читателя равнодушным. История любви прекрасной девушки-колдуньи и молодого барина одновременно трагична и прекрасна. Куприн создает сказочный образ полесской красавицы.
Мечта автора о сильной и бескорыстной любви (по повести А. И. Куприна «Гранатовый браслет»)	Сочинения.	Тема любви — основная в творчестве Куприна. По его мнению, именно любовь дает возможность раскрыться всем самым прекрасным сторонам человеческой души.
«Три правды» в пьесе А. М. Горького «На дне»	Сочинения.	В пьесе Горький противопоставляет гуманизм ложный, проповедующий всеобщее смирение, покорность судьбе, и подлинный гуманизм, суть которого — в борьбе против всего, что угнетает человека, лишая его достоинства и веры в свои силы, против рабской жизни человечества.
Признание в любви к Родине в поэзии С. А. Есенина	Сочинения.	Стихи Есенина всегда и для каждого человека будут полны той неизмеримой прелести, которая отличает для истинно русского человека истинно русские стихи.
Актуальность сатиры Маяковского	Сочинения.	Сатира Маяковского нацелена против всего того, что символизировало и продолжает символизировать застой, пошлость и отсталость, — не только в стране, но и во всем мире.
Образ родины в лирике А. А. Блока	Сочинения.	В творчестве Александра Блока тема Родины обретает особое звучание. Во многом это связано со временем, в которое довелось жить поэту. Начало века, Первая мировая война, революция — все это стало настоящим испытанием для России и живших в те годы людей.
Героизм русских женщин (по повести Б Л. Васильева «А зори здесь тихие.»)	Сочинения.	Великая Отечественная война — великая беда, беда страны, всего русского народа. Много лет прошло с той поры, но все еще живы в памяти события тех лет, живы во многом благодаря рассказам ветеранов и писателей, посвятивших себя и все свое творчество правде о войне, отголоски которой живы по сей день.
Юмор на страницах романа М. А. Шолохова «Поднятая целина»	Сочинения.	Человек, взявший в руки эту книгу, с первых же страниц начинает сопереживать героям, с волнением следить за тем, как развивается сюжет. Большую роль в создании столь экспрессивных и живых образов героев романа сыграл юмор.
Роман Е. И. Замятина «Мы»	Сочинения.	В романе поднимаются важнейшие проблемы человеческой жизни. Прежде всего это поиск счастья. Автор пишет роман в виде своеобразного дневника. В жанре антиутопии написано много известных произведений того периода, Замятин также прибегает к помощи этого жанра.
Добро и зло в романе М. А. Булгакова «Мастер и Маргарита»	Сочинения.	Роман М. А. Булгакова «Мастер и Маргарита» принес писателю заслуженную популярность и любовь читателей. Этот роман с самого момента своего создания вызывает огромное количество споров и нерешенных вопросов.
Интеллигенция и революция в романе Б. Л. Пастернака «Доктор Живаго»	Сочинения.	В своем знаменитом романе «Доктор Живаго» Борис Пастернак затронул важную для своей эпохи проблему роли революционных событий в судьбе русской интеллигенции и роли революции в истории России в целом.
Любовная лирика Марины Цветаевой (анализ одного стихотворения)	Сочинения.	Несмотря на то что Цветаева не желала писать о политике, пытаясь сосредоточиться только на внутреннем своем мироощущении, ей не удалось поместить в информационный вакуум свое творчество.
Отражение истории в лирике О. Э. Мандельштама	Сочинения.	Если в своих ранних поэтических произведениях Мандельштам любуется красотой природы, в них ощущается полная гармония поэта со всем миром, то позже происходит значительная переоценка красоты и романтического восприятия жизни. И на смену маленьким царствам и чудесам приходит «омут злого и вязкого».

Шпаргалки (шпора) по Математике.

Математика:
Обозначения	Математика.
Действия со степенями	Математика.	Для любых x, у € R и а >О, b > О имеют место равенства.
Формулы сокращенного умножения	Математика.
Преобразование арифметических корней	Математика.
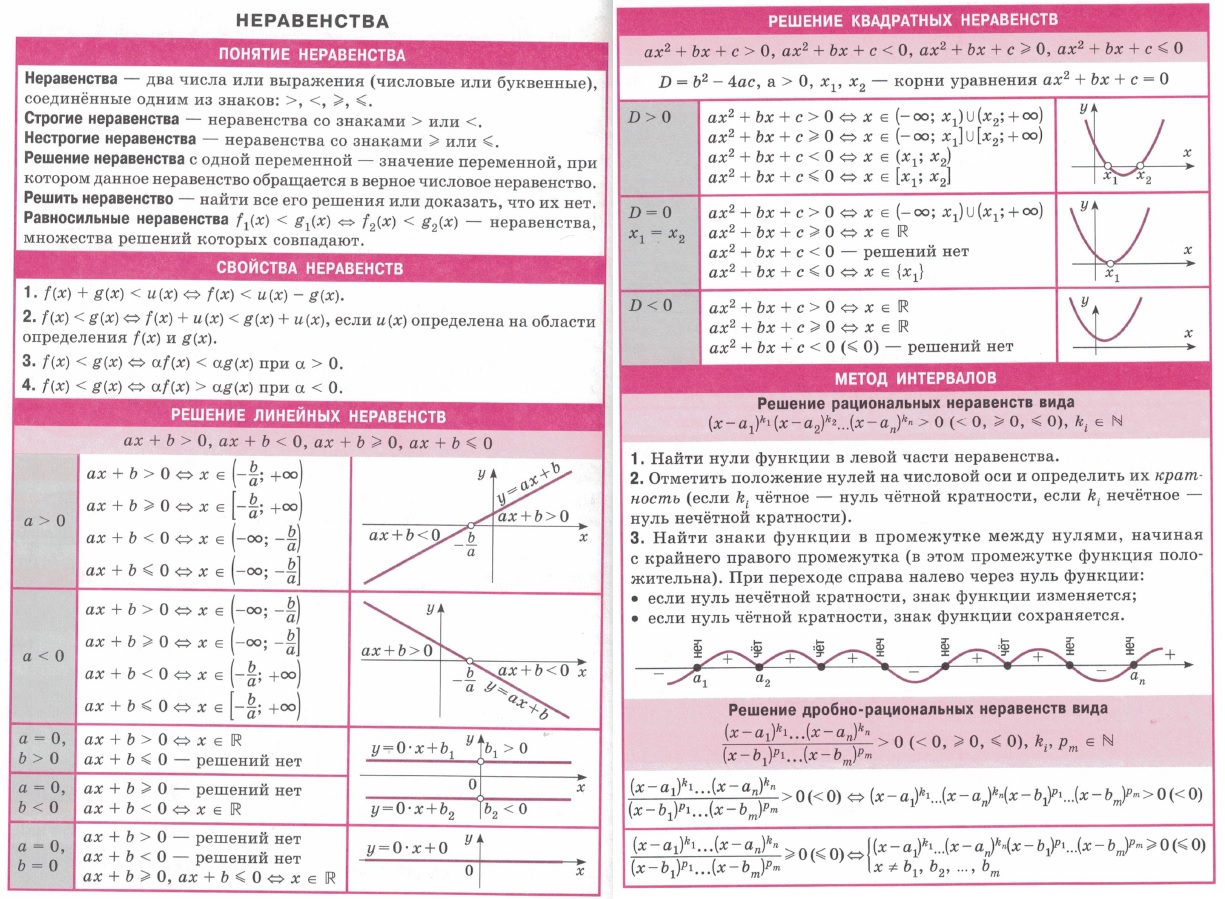
Числовые неравенства и их свойства	Математика.	По определению a < b, если a — b < 0. Неравенство b > a равносильно неравенству a < b. Это строгие неравенства.
Логарифмы и их преобразование	Математика.
Квадратное уравнение, квадратный трехчлен, формулы Виета	Математика.
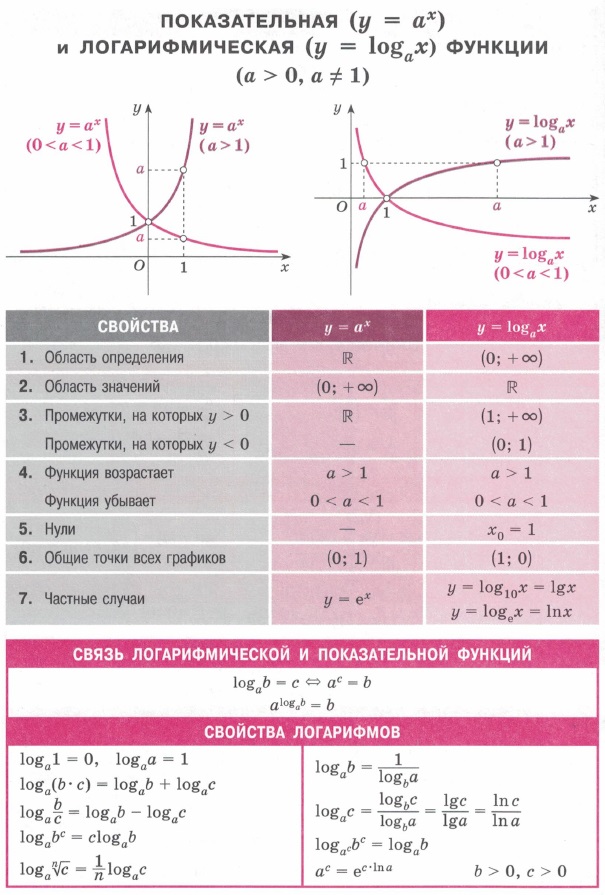
Показательная функция, ее свойства и график	Математика.	Показательная функция у = ax (а > 0) определена при всех x € R и обладает свойствами.
Логарифмическая функция, ее свойства и график	Математика.	Логарифмическая функция у = loga x (а > 0, a # 1 ) определена только при х > 0 (у = loga x <=> х = аy) и обладает следующими свойствами.
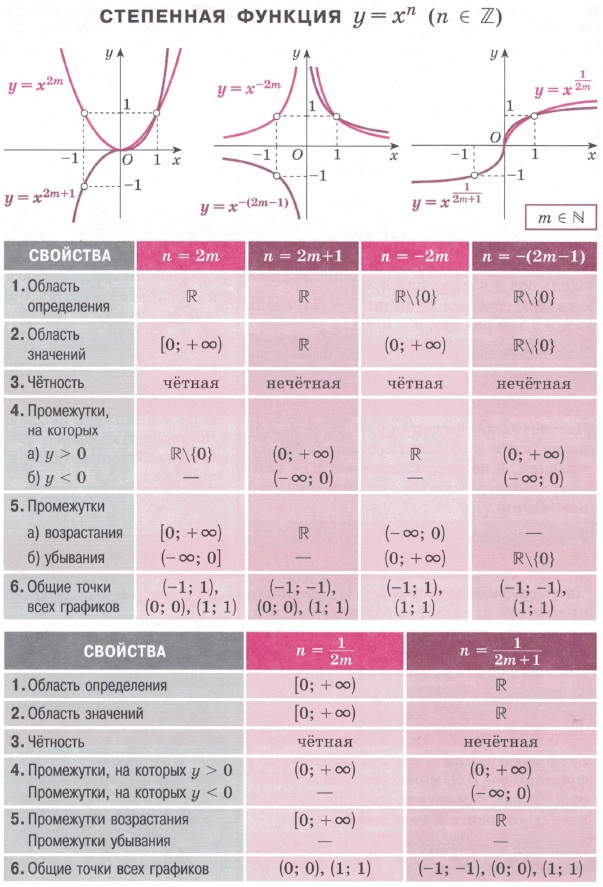
Области определения степенных функций	Математика.
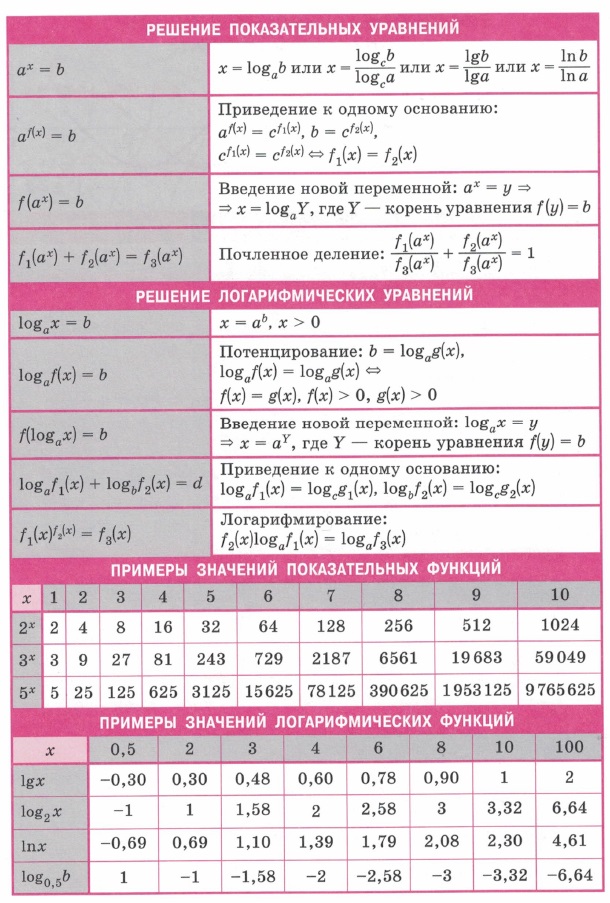
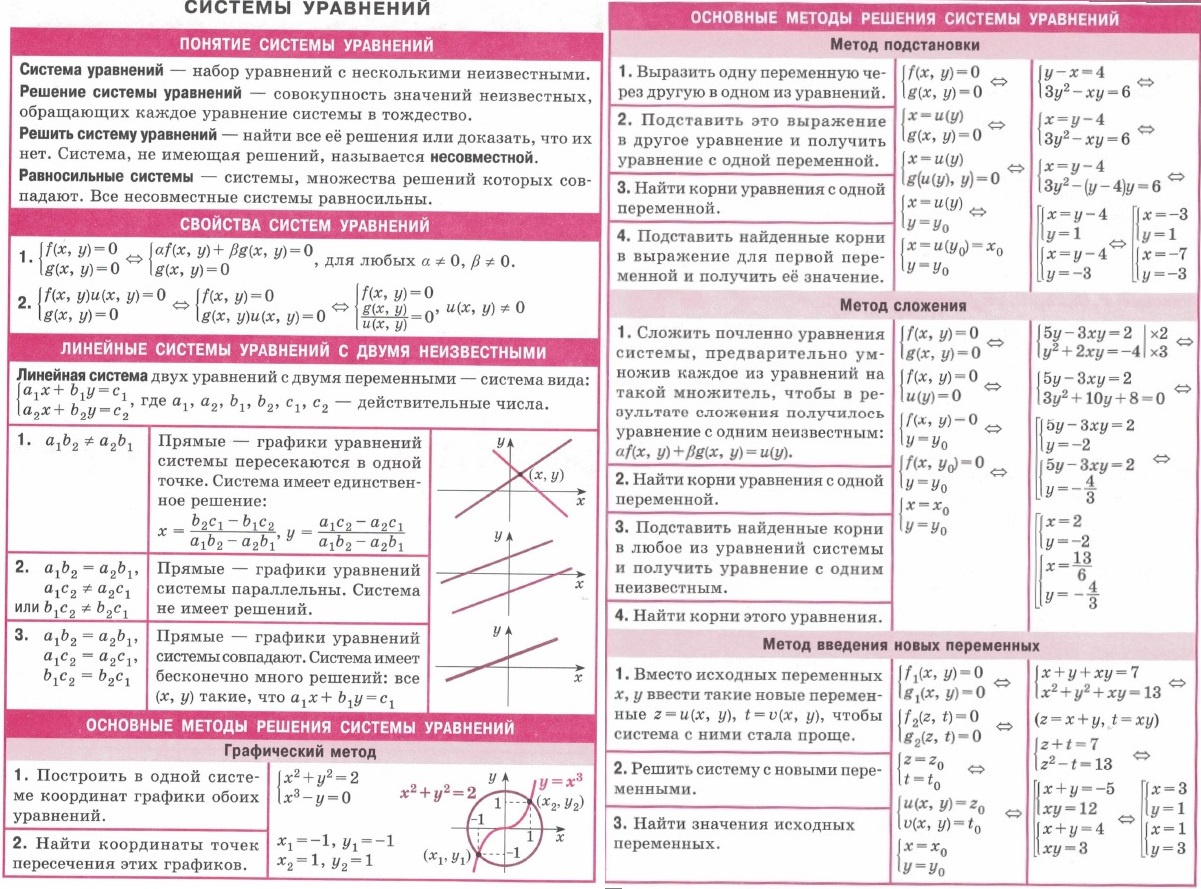
Решение уравнений	Математика.	При решении уравнении или неравенств чаше всего данное уравнение заменяется более простым равносильным уравнением. Паша цель состоит только в том, чтобы указать на некоторые наиболее эффективные такие замены.
Простейшие неравенства, содержащие знак модуля	Математика.	Простейшие неравенства с одним модулем можно решить способом раскрытия модуля но определению, по можно их свисти к простым системам или совокупности систем более коротким способом.
Иррациональные неравенства	Математика.	Основные иррациональные неравенства сводятся к системе или совокупности систем рациональных неравенств. Здесь мы ограничимся двумя неравенствами, содержащими только квадратные корни.
Показательные неравенства	Математика.	Решения основных показательных неравенств, помешенных в таблице, вытекают из свойств монотонности показательной функции. Ниже X — неизвестная или выражение.
Логарифмические неравенства	Математика.	Решения основных логарифмических неравенств, пометенных в таблице, вытекают из свойств монотонности логарифмической функции. Ниже X — неизвестная или выражение, М > О, N > 0.
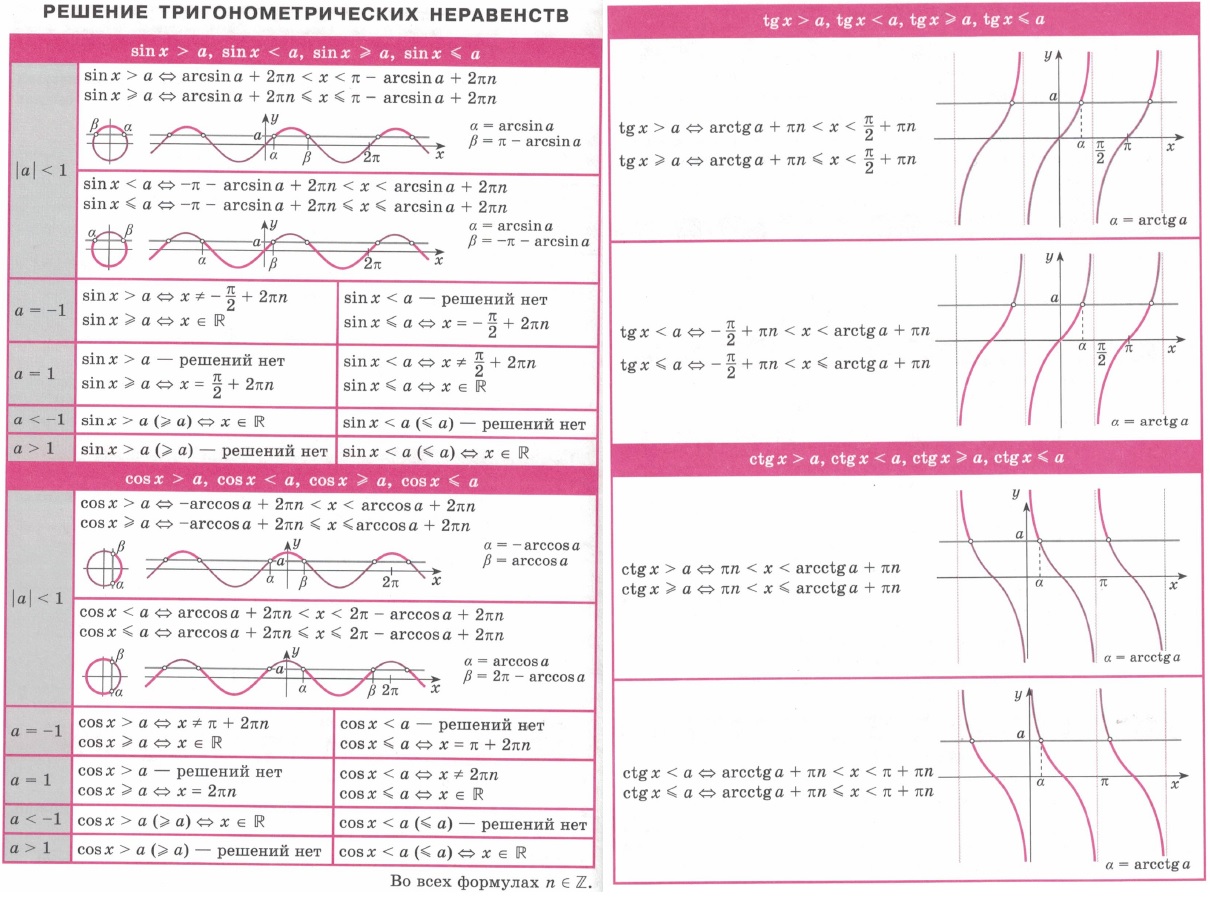
Решение неравенств. Метод интервалов	Математика.	Целесообразно описать волну знаков стандартной рациональной функции и применение ее к методу интервалов.
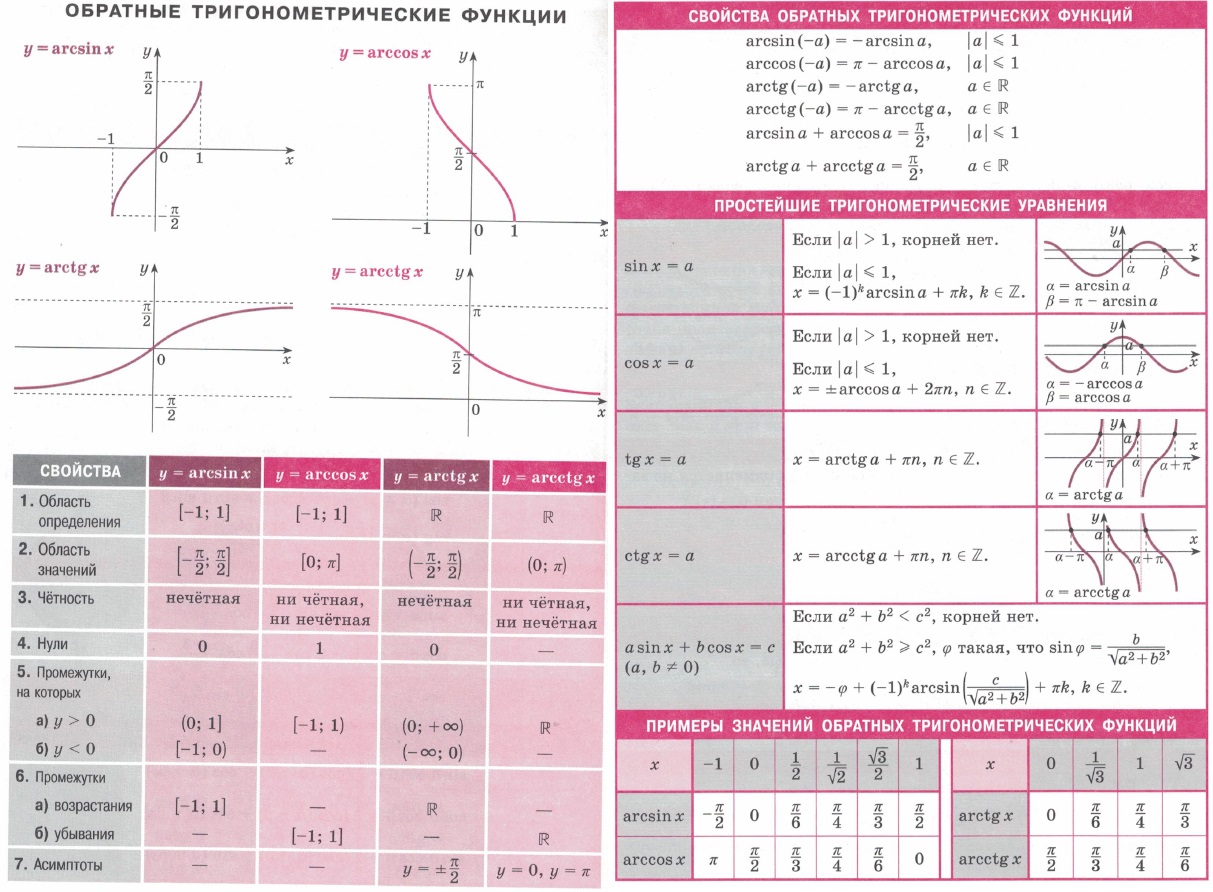
Определение тригонометрических функций	Математика.
Свойства тригонометрических функций	Математика.
Тригонометрические формулы	Математика.
Основные тригонометрические уравнения	Математика.	Простейшие тригонометрические уравнения в общем случае решаются ни следующим формулам.
Основные определения, теоремы и формулы планиметрии	Математика.
Основные сведения из стереометрии	Математика.	Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей и этой плоскости.
Метод координат	Математика.
Векторы	Математика.	Вектором называется направленный отрезок. Длина соответствующего отрезка называется модулем вектора.
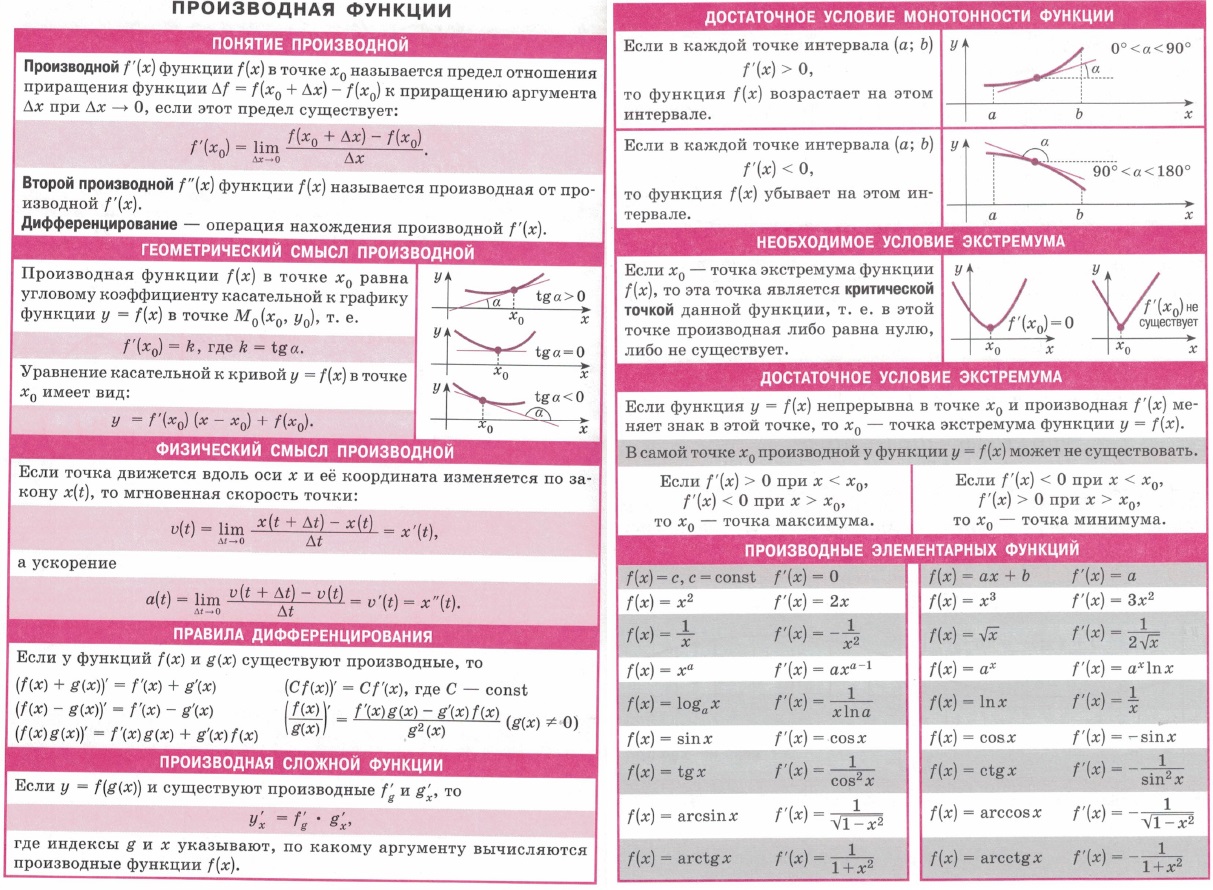
Дифференцирование	Математика.	Нахождение производных (дифференцирование) функций выполняется по определенным формулам и правилам, доказываемым в соответствующих учебниках.
Применение первой производной	Математика.
Последовательность. Прогрессии	Математика.
Интегрирование	Математика.
Взаимное расположение двух прямых в пространстве	Математика.	Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
Касательная плоскость к шару	Математика.
Взаимное расположение двух плоскостей (формулировки и примеры)	Математика.	Взаимное расположение двух плоскостей характеризуется двумя возможностями.
Перпендикулярность прямой и плоскости	Математика.
Взаимное расположение прямой и плоскости в пространстве (формулировки и примеры)	Математика.
Объем цилиндра	Математика.
Свойства параллельных плоскостей	Математика.	Две плоскости, перпендикулярные одной прямой, параллельны.
Теорема о боковой поверхности прямой призмы	Математика.	Многогранник, составленный из двух равных многоугольников А1, А2 ... Аn и В1, В2,... Вn, расположенных в параллельных плоскостях и n параллелограммов, называется призмой.
Перпендикуляр и наклонная плоскости	Математика.
Свойство противолежащих граней параллелепипеда	Математика.
Расстояние между скрещивающимися прямыми (формулировка и пример)	Математика.	Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, и он перпендикулярен каждой из этих прямых.
Площадь боковой поверхности конуса	Математика.
Угол между скрещивающимися прямыми (формулировка и пример)	Математика.	Любые две пересекающиеся прямые расположены в одной плоскости и образуют две пары смежных углов. Меньший из этих углов называется углом между пересекающимися прямыми.
Угол между прямой и плоскостью (формулировка и пример)	Математика.
Объем призмы	Математика.
Объем пирамиды	Математика.	Объем пирамиды равен одной третьей произведения площади основания пирамиды на длину ее высоты.
Угол между двумя плоскостями (формулировка и пример)	Математика.
Площадь сферы	Математика.	Около сферы можно описать многогранник с достаточно большим числом граней, объем которого будет достаточно точно выражать объем шара (равного ), а площадь боковой поверхности многогранника — площадь сферы.
Двугранный угол. Линейный угол двугранного угла (формулировка и примеры)	Математика.	Две полуплоскости, имеющие общую граничную прямую и не лежащие в одной плоскости, называются двугранным углом. Эти полуплоскости называются гранями двугранного угла, а их общая граничная прямая — ребром угла.
Теорема о боковой поверхности правильной пирамиды	Математика.	Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника. Под центром многоугольника понимается центр вписанной или описанной окружностей.
Трехгранный и многогранный углы (формулировки и примеры)	Математика.
Площадь боковой поверхности цилиндра	Математика.
Призма	Математика.	Призма — частный случаи многогранника. Для получения призмы необходимо взять два многоугольника в плоскостях || , причем многоугольники должны быть совмещенными при параллельном переносе, и соответствующие вершины соединить отрезками.
Признак перпендикулярности плоскостей	Математика.	Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром: пары вертикальных углов равны, а сумма двух смежных углов равна 180°. Если один из четырех углов прямой, то три остальных также равны и прямые. Две плоскости называются перпендикулярными, если угол между ними прямой.
Прямая и правильная призма (формулировки и примеры)	Математика.
Свойства перпендикулярных прямой и плоскости (доказательство одного из них)	Математика.
Параллелепипед. Прямоугольный параллелепипед (формулировки и примеры)	Математика.	Параллелепипед можно считать пространственным аналогом параллелограмма. Параллелепипед — это четырехугольная призма, у которой все грани — параллелограммы. Параллелепипед называется прямоугольным, если все его грани прямоугольники.
Признак параллельности плоскостей	Математика.	Две плоскости называются параллельными, если они не пересекаются (не имеют общих точек). Признак параллельности двух плоскостей выражается следующей теоремой.
Пирамида	Математика.
Объем конуса	Математика.
Правильная пирамида (формулировки и примеры)	Математика.
Цилиндр	Математика.
Свойства изображения пространственных фигур на плоскости	Математика.	Пространственные фигуры мы изображаем на плоскости (на бумаге, доске и пр.), используя параллельное проектирование.
Признак параллельности прямой и плоскости	Математика.	Прямая и плоскость называются параллельными, если они не пересекаются (не имеют общих точек).
Конус (формулировки и примеры)	Математика.
Признак параллельности прямых	Математика.	Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Через точку вне данной прямой можно пронести прямую, параллельную этой пряиой, и притом только одну.
Сфера и шар (формулировки и примеры)	Математика.	Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
Теорема о трех перпендикулярах	Математика.
Задача 1	Математика.	В правильной четырехугольной пирамиде высота равна 12 см. а апофема — 15 см. Найти боковое ребро.
Задача 2	Математика.	Прямоугольный треугольник, гипотенуза которого равна 17 см, а один из катетов — 8 см, вращается около этого катета. Найдите площадь поверхности тела вращения.
Задача 3	Математика.	В правильной треугольной пирамиде боковое ребро равно 4 см. а сторона основания — 6 см. Найдите объем пирамиды.
Задача 4	Математика.	Образующая конуса, наклонена к плоскости основании под углом 30°, а его высота раина 12 см. Найдите площадь его боковой поверхности.
Задача 5	Математика.	Найдите площадь сечения шара радиуса 41 см, проведенною на расстоянии 9 см от центра.
Задача 6	Математика.	В основани пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 15 см, а один Hi катетом — 9 см, Найдите площадь сечения, проведенною через середину высоты пирамиды параллельно ее основанию.
Задача 7	Математика.	В правильной четырехугольной пирамиде сторона основания равна 10 см, а высота — 12 см. Найдите площадь полной поверхности пирамиды.
Задача 8	Математика.	Высота прямой призмы равна 10 см, а ее основанием является прямоугольник, стороны которого равны 8 см и 6 см. Найдите плошадь диагонального сечения.
Задача 9	Математика.	В правильной четырехугольной пирамиде высота равная 7 см, а боковое ребро наклонено к плоскости основания под углом 45°. Найдите объем пирамиды.
Задача 10	Математика.	Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
Задача 11	Математика.	Основание четырехугольной призмы — квадрат со стороной 10 см, высота призмы 12 см. Диагональное сечение разбивает данную призму на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
Задача 12	Математика.	Радиус основания конуса равен 14 см. Найдите площадь сечения, проведенного перпендикулярно его оси через ее середину.
Задача 13	Математика.	Шар с центром в точке О касается плоскости и точке A. Точка лежит и плоскости касания. Найдите объем шара. если AB = 21 см. а BO = 29 см.
Задача 14	Математика.	Сферу на расстоянии 8 см от центра пересекает плоскость. Радиус сечения ранен 15 см. Найдите площадь сферы.
Задача 15	Математика.	В правильной треугольной призме ABCA1B1C1 проведено сечение через вершину С1и ребро АB. Найдите периметр сечения. Если сторона основании равна 24 см, а боковое ребро = 10 см.
Задача 16	Математика.	Осевым сечением цилиндр является, квадрат, диагональ которого равна см. Найдите площадь поверхности цилиндра.
Задача 17	Математика.	В основании прямого параллелепипеда лежит ромб, диагонали которого равны 12 см и 16 см. Высота параллелепипеда равна 8 см. Найдите площадь его полной поверхности.
Задача 18	Математика.	В прямоугольном параллелепипеде стороны основания равны 5 см и 12 см, а диагональ параллелепипеда наклонена к плоскости основания под углом 45°. Найдите высоту параллелепипеда.
Задача 19	Математика.	В правильной четырехугольной пирамиде сторона основания равна 12 см, а апофема — 15 см. Найдите боковое ребро пирамиды.

Шпаргалки (шпора) по Физике.

Физика:
Буквы, используемые для обозначения величин	Физика.	A — работа; В — магнитная индукция; С — электроемкость конденсатора; D — оптическая сила; Е — напряженность электрического поля, энергия (в электростатике W); F — сила, фокусное расстояние линзы, постоянная Фарадея; K — Кельвин и т.п.
Методика решения задач по физике	Физика.	Внимательно прочитать условие задачи, уяснить, какой физический процесс или явление в ней описывается.
Векторы	Физика.	Вектор — это величина, определяемая не только численным значением, но и направлением в пространстве, например сила, скорость , ускорение и т.д.
Основные положения, законы и формулы (механика)	Физика.	Механика — раздел физики, изучающий механическое движение. Она содержит три раздела.
Кинематика	Физика.	Абсолютно твердое тело — это тело, взаимное расположение частиц которого при движении не меняется.
Динамика	Физика.	Сила — это векторная величина, характеризующая действие одного тела на другое и сообщающая ускорение или деформацию последнему.
Статика	Физика.	Равновесие — это сохранение телом состояния покоя или равномерного прямолинейного его движения с течением врсмени.
Простые механизмы	Физика.	Рычаг — тело, вращающееся вокруг некоторой оси.
Жидкости и газы	Физика.	Гидростатический парадокс: давление, оказываемое жидкостью на дно сосуда, не зависит от формы сосуда и определяется только уровнем жидкости в сосуде.
Молекулярная физика	Физика.	Основные положения молекулярно-кинетической теории (МКТ).
Термодинамика	Физика.	Термодинамика — раздел физики, рассматривающий явления, связанные с взаимопревращением механической и внутренней энергий и передачей внутренней энергии от одного тела к другому.
Электростатика	Физика.
Электричество	Физика.
Магнитное поле	Физика.
Колебания и волны	Физика.
Оптика	Физика.
Элементы теории относительности	Физика.	Релятивистская механика изучает законы движения при скоростях, близких к скорости света.
Квантовая физика	Физика.	Фотоэффект — явление вырывания электронов с поверхности металла под действием света (внешний фотоэффект, в полупроводниках — внутренний).
Атомная и ядерная физика	Физика.	Ядерные реакции — превращения одних атомных ядер в другие при взаимодействии их с элементарными частицами или друг с другом.
Шкала электромагнитных волн	Физика.
Десятичные приставки к единицам СИ	Физика.
Единицы физических величин	Физика.
Таблица основных физических констант	Физика.
Международная система единиц (СИ)	Физика.

Шпаргалки (шпора) по Химии.

Химия:
Основные понятия химии	Химия.	Химия — наука, изучающая состав, строение, свойства, получение и превращения веществ.
Основные положения атомно-молекулярной теории	Химия.	Все веществ состоят v молекул. Молекула — это наименьшая частица вещества, сохраняющая свойства тогo вещества. Молекулы разрушаются при химических реакциях.
Относительная атомная масса	Химия.	Относительной атомной массой (Аг) называется масса одного атома, выраженная в атомных единицах массы (а. е. м.).
Молекулярная масса и Молярная масса	Химия.	Молекулярная масса — это масса одной молекулы вещества, выраженная в атомных единицах массы.
Атомная масса	Химия.	За единицу атомной массы принята атомная единица массы (а. е. м.). Это 1/12 часть массы изотопа углерода с массовым числом 12.
Закон постоянства состава	Химия.	Согласно закону постоянства состава, всякое чистое вещество имеет постоянный состав независимо от способа его получения. Так, оксид кальция можно получить следующими способами.
Строение атома. Химическая связь	Химия.	Атомная орбиталь — часть пространства вокруг ядра атома, в которой вероятность нахождения данного электрона наибольшая (90%).
Энергетический уровень и подуровень	Химия.	Энергетический уровень — это совокупность орбиталей, которые имеют одинаковые значения главного квантового числа. Число энергетических уровней атома равно номеру периода, в котором он расположен.
Принцип Паули	Химия.	В атоме не может быть двух электронов с одинаковым набором всех четырех квантовых чисел.
Характеристика 4 квантовых чисел	Химия.	Главное квантовое число (n) — характеризует энергию и размер орбитали.
Правило Гунда	Химия.	Электроны, заполняющие данный энергетический уровень, стремятся занять максимальное количество орбиталей, располагаясь на каждой по одному, чтобы суммарный спин был максимален.
Электронная конфигурация	Химия.	Электронная конфигурация — это конкретное распределение электронов по орбита-лям атома. Электронная конфигурация атома записывается с помощью электронного уравнения.
Энергия ионизации	Химия.	Энергия ионизации (мера проявления металлических свойств) — это энергия, необходимая для отрыва электрона от атома.
Электронная конфигурация атома	Химия.	Для изображения конфигурации атома (строения электронных оболочек) необходимо знать.
Типы химических связей	Химия.	Электроотрицательность — мера способности атома, связанного с другим атомом, притягивать к себе электроны.
Валентность	Химия.	Валентность — это способность атома соединяться с другими атомами. С точки зрения теории строения атомов валентность определяется числом химических связей (или числом общих электронных пар), которыми данный атом соединен с другими.
Степень окисления	Химия.	Степень окисления — это условный заряд атома в молекуле, если считать, что все молекулы состоят из ионов. Степень окисления рассчитывается алгебраически, учитывая, что сумма положительных и отрицательных зарядов в молекуле равна нулю.
Кристаллические и аморфные вещества. Их различие	Химия.	В кристаллических веществах атомы расположены в строгом порядке — в узлах кристаллической решетки. В аморфных веществах атомы расположены беспорядочно, так же, как и в жидкостях.
Температура плавления веществ	Химия.	Температура плавления веществ с различными кристаллическими решетками.
Растворы	Химия.	Растворы — это однофазные системы переменного состава, состоящие из нескольких компонентов, один из которых является растворителем, а другие — растворенными веществами.
Диспергирование	Химия.	Диспергирование означает дробление. При растворении вещества измельчаются, то есть дробятся. Поэтому истинные и коллоидные растворы, а также взвеси (суспензии и эмульсии) относят к дисперсным системам.
Строение коллоидных частиц	Химия.	Коллоидные частицы имеют сложное строение. Они состоят из ядер и адсорбированных и притянутых ионов.
Истинные растворы	Химия.	Истинные растворы прозрачные. Отдельные частицы (молекулы, ионы) нельзя обнаружить даже при помощи ультрамикроскопа. Они не осаждаются и не задерживаются фильтрами.
Концентрация	Химия.	Концентрация — это содержание растворенного вещества в определенном количестве или объеме раствора. Массовая доля растворенного вещества (w) выражается в долях единицы и показывает массу растворенного вещества в определенной массе раствора.
Скорость химических реакций	Химия.	Под скоростью химической реакции понимают изменение концентрации реагирующих или образующихся веществ в единицу времени, то есть.
Химическое равновесие	Химия.	Химическое равновесие наступает при условии, когда скорости прямой и обратной реакций равны. Например, если в реакции.
Катализаторы	Химия.	Вещества, которые ускоряют химические реакции, но сами при этом не расходуются, называются катализаторами. Например, разложение бертолетовой соли и перокси-да водорода ускоряется в присутствии оксида марганца (IV).
Принцип Ле-Шателье	Химия.	Если на систему, которая находится в состоянии динамического равновесия, оказывать внешнее воздействие, то в системе будут протекать процессы, направленные на уменьшение этого внешнего воздействия.
Экзотермические реакции	Химия.	Экзотермические реакции — это реакции, происходящие с выделением теплоты. Эндотермические реакции — это реакции, происходящие с поглощением теплоты.
Примеры экзотермичеких и эндотермических реакций	Химия.	Химические уравнения показывают, какие вещества и в каких соотношениях вступают в реакцию и какие вещества и в каких соотношениях при этом образуются.
Электролитическая диссоциация	Химия.	Электролитической диссоциации подвергаются полярные молекулы. Как правило, это молекулы с ионной или ковалентной полярной связью.
Основные индикаторы	Химия.	Понятия «сильный электролит» и «сильная кислота»; «сильный электролит» и «сильное основание».
Классы неорганических веществ	Химия.	Задача. Даны оксиды: MgO, ZnO, CO2, N203, CuO, Аl203, Р205, SO3. Напишите формулы соответствующих гидроксидов и назовите их.
Сравнительная характеристика основных и кислотных оксидов	Химия.	Сравнительная характеристика основных и кислотных оксидов.
Гидролиз солей	Химия.	Гидролиз солей — взаимодействие ионов соли с водой, в результате которого образуются малодиссоциируемые соединения (ионы или молекулы) и изменяется реакция среды.
Подчинение гидролиза солей принципу Ле-Шателье	Химия.	Гидролиз солей — обратимый процесс. Для него, как и для любой другой обратимой реакции, характерно состояние равновесия, которое может смещаться по принципу Ле-Шателье.
Окислительно-восстановительные реакции	Химия.	Окислительно-восстановительные реакции — это реакции, которые протекают с изменением степеней окисления элементов.
Важнейшие восстановители и их свойства	Химия.	Восстановителями могут быть атомы всех элементов, кроме инертных газов и фтора. Но сильными восстановителями являются металлы. Металлы имеют на внешнем уровне один, два или три электрона, которые легко отдают, проявляя при этом свойства восстановителя.
Важнейшие окислители и их свойства	Химия.	Атомы элементов, имеющие на внешнем уровне шесть, семь электронов, легко принимают недостающие до восьми электроны, проявляя свойства окислителей.
Метод составления окислительно-восстановительных реакций	Химия.	Задача. Составьте уравнение окислительно-восстановительной реакции между хлоридом железа (III) FeCl3 и иодоводородом HJ, зная, что в результате реакции выделяется иод.
Основные принципы ряда напряжения металлов	Химия.	Чем меньше алгебраическая величина потенциала, тем выше восстановительная способность атомов этого металла. Как следует из ряда стандартных электродных потенциалов, металлический литий — самый сильный восстановитель в растворе, а золото — самый слабый.
Cтандартные электродные потенциалы	Химия.	Ряд стандартных электродных потенциалов составлен в порядке увеличения алгебраического значения стандартных , электродных потенциалов металлов Е0.
Неметаллы. Водород	Химия.	Все неметаллы являются р-элементами, то есть имеют не полностью застроенные р-орбитали. Они занимают в периодической системе правый верхний угол, образуя треугольник, вершиной которого является фтор, а основанием — линия, соединяющая элементы бор и астат.
Кислородные и водородные соединения неметаллов по периодической системе	Химия.	Высшие оксиды неметаллов являются кислотными. Сила соответствующих им кислот увеличивается от IV к VII группе.
Изменение электроотрицательности неметаллов в периодической системе	Химия.	Все неметаллы характеризуются высокой электроотрицательностью: для них характерна способность притягивать электроны других элементов при образовании молекул.
VII группа элементов. Главная подгруппа, галогены. Хлор и его соединения	Химия.	Возможные валентности галогенов с точки зрения строения атома.
Изменение окислительно-восстановительных свойств галогенов	Химия.	Так как все галогены имеют на внешнем электронном слое семь электронов, то они являются сильными окислителями. Но в группе сверху вниз с увеличением радиуса атома уменьшаются окислительные свойства и увеличиваются восстановительные свойства.
Свойства хлороводородной кислоты с позиций ионных реакций и теории окисления-восстановления	Химия.	Хлороводородная кислота является сильным электролитом. В растворе она почти полностью диссоциирует.
VI группа элементов. Главная подгруппа. Кислород, сера и их соединения	Химия.	Сходство и различие свойств элементов VI группы, главной подгруппы с точки зрения строения атома.
Электронные конфигурации атомов	Химия.	Наличие двух неспаренных электронов на наружном энергетическом уровне указывает на валентность 2 в невозбужденном состоянии. Сравнение строения внешних уровней показывает, что у S, Se, Те и Ро, в отличие от кислорода, имеются вакантные орбитали d-подуровня.
Биологическое значение кислорода и его соединений	Химия.	Кислород в организме человека 62,4% по массе. Организм взрослого человека в состоянии покоя потребляет 264 см3 кислорода в минуту. Кислород участвует во всех видах обмена веществ в организме.
Биологическое значение серы и ее соединений	Химия.	В организме человека 0,16% серы. Суточная потребность взрослого человека 4-5 г серы. Сера входит в состав белков, аминокислот, пептидов, гормонов, некоторых витаминов.
V группа элементов. Главная подгруппа	Химия.	Химические свойства азота.
Электронное строение, химические свойства, способ обнаружения	Химия.	Электронное строение, химические свойства, способ обнаружения.
IV группа элементов. Главная подгруппа. Углерод, кремний и их соединения	Химия.	Общая характеристика четвертой группы главной подгруппы.
Металлы и их соединения	Химия.	Уравнения реакций отношения металлов.
Гипс	Химия.	Различают следующие виды гипса: природный CaSO4 • 2H20, жженый (CaSO4) 2 • Н20, безводный CaSO4. Жженый (полуводный) гипс, или алебастр, (CaSO4) 2 • Н20 получают при нагревании природного гипса до 180°С.
Алюминий	Химия.	Алюминий Аl находится в третьем периоде, третьей группе, главной подгруппе периодической системы. Его порядковый номер равен 13. Электронная конфигурация атома Is22s22p63s23p6.
Сходство и отличие свойств элементов главной и побочной подгруппы I группы	Химия.	Калий — элемент главной подгруппы, медь — элемент побочной подгруппы. У калия и меди одинаковое строение внешнего электронного слоя — 1 электрон на четвертом электронном слое.
Свойства меди	Химия.	Физические свойства. Металл красноватого цвета, температура плавления 1083°С, плотность 11,3 г/см3; очень хороший проводник тепла и электрического тока.
Способность соединений меди (II)	Химия.	Если к раствору сульфата меди (II) прилить раствор аммиака, то выпадает голубой осадок основной соли, который легко растворяется в избытке аммиака, окрашивая жидкость в интенсивный синий цвет.
Углеводороды	Химия.	Гибридизация — это смешивание валентных электронных облаков и образование качественно новых, равноценных гибридных валентных электронных облаков.
Метан	Химия.	Метан — химически малоактивное вещество. Наиболее характерны реакции замещения.
Этилен	Химия.	Этилен — химически активное вещество.
Ацетиленовые углеводороды	Химия.	Ацетиленовыми называются углеводороды, в молекулах которых имеется тройная связь между атомами углерода.
Химические свойства углеводородов	Химия.	Химические свойства, характерные для углеводородов, содержащихся в молекулах.
Диеновые углеводороды	Химия.	Особенность диеновых углеводородов в том, что присоединение происходит по концам цепи, а между вторым и третьим атомами углерода образуется двойная связь.
Полимеры	Химия.	Полимеры синтезируют полимеризацией и поликонденсацией. Реакция полимеризации — это процесс соединения молекул в более крупные молекулы.
Бензол	Химия.	В бензоле все атомы углерода находятся во втором валентном состоянии (sр2-гибридизация).
Свойства ацетилена	Химия.	Свойства ацетилена, на основании которых он применяется в органических синтезах.
Способы получения бензола, толуола, этилбензола, стирола	Химия.	Получение бензола.
Формула предельного углеводорода	Химия.	Формула предельного углеводорода, содержащего.
Виды изомерии	Химия.	Виды изомерии.
Этиловый спирт	Химия.	Органические соединения, содержащие гидроксильную группу (ОН), связанную с атомом углерода, находящимся в состоянии sр3-гибридизации, называются одноатомными предельными спиртами.
Фенол	Химия.	Фенол проявляет слабые кислотные свойства. Под влиянием группы ОН электронная плотность перераспределяется в бензольном кольце таким образом, что увеличивается у второго, четвертого и шестого , атомов углерода. В результате происходит замещение атомов водорода в орто и пара положениях.
Взаимное влияние гидроксигрупп в многоатомных спиртах	Химия.	Так как в глицерине три группы ОН, в отличие от одноатомных спиртов, химическая активность глицерина выше, чем одноатомных спиртов. В реакциях могут участвовать одна, две или все три гидроксигруппы.
Третичный спирт	Химия.	Третичным называют спирт, в котором функциональная группа ОН связана с третичным углеродным атомом, например.
Уксусный альдегид	Химия.	Атом углерода в карбони-ле находится в sр2-гибридизации. В результате образуются три —> связи. Такие связи лежат в одной плоскости и углы между ними 120°.
Электронное строение карбоксильной группы	Химия.	Карбоксильная группа.
Уксусная кислота	Химия.	Уксусная кислота, свойства, отношение.
Муравьиная кислота: химические свойства	Химия.	От остальных карбоновых кислот муравьиная кислота отличается тем, что карбоксильная группа в ней связана не с углеводородным радикалом, а с атомом водорода. Поэтому муравьиную кислоту можно рассматривать и как кислоту, и как альдегид.
Жиры	Химия.	Животные жиры твердые, так как образованы высшими предельными карбоновыми кислотами. Например, тристеарин (тристеарат глицерина).
Глюкоза	Химия.	Глюкоза является альдеги-доспиртом, так как атомы углерода связаны между собой сигма-связью, возможно в ращение частей молекулы относительно сигма-связей.
Крахмал и клетчатка (целлюлоза)	Химия.	Крахмал и клетчатка являются природными полимерами глюкозы. Крахмал -полимера-глюкозы, клетчатка — полимер --> глюкозы.
Амины. Строение. Химические свойства	Химия.	В молекуле метиламина все связи ковалентные полярные. Азот имеет неподеленную пару электронов, с помощью которой притягивает катион Н из воды и кислоты, проявляя основные свойства.
Диэтиламин, анилин, аммиак, эгиламин, метиламин, дифениламин	Химия.	Радикалы — алкины, заместители рода, доноры электронов. Электронная плотность от них смещается на азот аминогруппы, который имеет неподеленную пару электронов, за счет которых аминогруппа проявляет основные свойства.
Аминокислоты	Химия.	Аминокислоты — это вещества, в молекулах которых содержатся одновременно аминогруппы — NH2 и карбоксильная группа — СООН. Общая формула аминокислот может быть представлена следующим образом.
Органические соединения с двойственными химическими функциями	Химия.	Аминокислоты обладают свойствами кислот.
Белки	Химия.	Первичная структура белка — это порядок соединения аминокислот в полипептидной цепи.
Денатурация белка	Химия.	Денатурация белка — это разрушение третичной и вторичной структуры белка. Она может быть вызвана нагреванием, действием радиации, встряхиванием. Денатурация белка происходит при варке яиц, приготовлении пищи и т. д.
Роль водородных связей в построении белковой молекулы	Химия.	В природных волокнах макромолекулы целлюлозы располагаются в одном направлении: они ориентированы вдоль оси волокна. Возникающие при этом многочисленные водородные связи между гидроксильными группами макромолекул обусловливают высокую прочность этих волокон.
Гетероциклические соединения	Химия.	Гетероциклические соединения можно разделить на следующие группы.
Основные химические свойства пиррола	Химия.	Вследствие участия пары неподеленных электронов атома азота пиррола в ароматическом сопряжении гетероатом становится более бедным электронами, поэтому пиррол проявляет слабокислотные свойства.
Нуклеиновые кислоты. Нуклеотиды	Химия.	Структурные формулы азотистых оснований нуклеиновых кислот, производные пиримидина.
Структурные формулы азотистых оснований нуклеиновых кислот, производные пурина	Химия.	Структурные формулы азотистых оснований нуклеиновых кислот, производные пурина.
Структурные формулы углеводов, входящих в состав нуклеиновых кислот	Химия.	В состав РНК входит D-рибоза, ДН — D-2-дезоксирибоза, которые в цепи нуклеиновых кислот существуют в циклической B-D-фуранозной форме.
Общая схема гидролиза нуклеиновых кислот (НК)	Химия.	Общая схема гидролиза нуклеиновых кислот (НК).
Виды нуклеиновых кислот	Химия.	В зависимости от состава и ФУНКЦИЙ, выполняемых в клетке, различают.

Шпаргалки (шпора) по Биологии.

Биология:
Растительная клетка, ее строение	Биология.	Типичная растительная клетка содержит хлоропласты и вакуоли и окружена целлюлозной клеточной стенкой. Плазматическая мембрана (плазмалемма), окружающая растительную клетку, состоит из двух слоев липидов и встроенных в них молекул белков.
Корень	Биология.	Корень — подземная часть вегетативного тела растения, закрепляющая его в почве. Появился впервые у сосудистых растений.
Побег, лист, стебель	Биология.	Побег — это надземная часть растения. Вегетативный побег закладывается в процессе развития зародыша, в котором он Представлен почечкой. Почечка — это стебелек и листовые зачатки, может считаться первой почкой растения.
Цветок — видоизмененный побег	Биология.	Цветок — это укороченный и ограниченный в росте побег, выполняющий генеративную функцию. Состоит из: цветоножки, цветоложа с чашелистиками и лепестками (околоцветник), а также тычинок и плодолистиков.
Размножение растений	Биология.	Размножение — это воспроизведение особями себе подобных. Оно позволяет поддерживать преемственность между поколениями и поддерживать численность популяций на определенном уровне.
Опыление. Оплодотворение	Биология.	Опыление — это процесс переноса пыльцы с пыльника на рыльце пестика у цветковых растений и на микрополе семязачатка голосеменных. Опыление предшествует оплодотворёнию.
Строение семян. Прорастание и распространение	Биология.	Главная часть семени — зародыш. Он состоит из корешка, стебелька, почечки и двух или одной семядолей. Этот признак лежит в основе разделения всех цветковых растении на два класса — Двудольные и Однодольные.
Развитие растительного мира	Биология.	Многообразие существующих ныне и живших ранее на Земле растений является результатом эволюционного процесса. Современная классификация растений дает представление о пути становления тех или иных систематических групп.
Водоросли	Биология.	Это низшие хлорофиллсодержащие растения, не расчлененные на стебель, корень и листья. Обитают преимущественно в пресных водоемах и морях.
Бактерии	Биология.	Это мельчайшие организмы, обладающие клеточным строением, не имеющие настоящего оформленного ядра. Бактерии освоили самые разнообразные среды обитания: почву, воду, воздух, внутреннюю среду организмов.
Лишайники	Биология.	Это симбиотическая ассоциация гриба и водоросли. Гриб в этом случае либо сумчатый, либо базидиальный, а водоросль либо зеленая, либо сине-зеленая. Поселяются лишайники обычно на голых скалах или стволах деревьев.
Мхи	Биология.	Это наиболее примитивные из групп наземных растений. Они мало приспособлены к жизни на суше, поэтому привязаны к влажным, затененным местам.
Папоротники	Биология.	Это сосудистые растения: спорофит преобладает над гаметофитом. Встречаются чаще во влажных тенистых местах. Листья (вайи) спорофита достигают высоты до 1 м и растут от толстого горизонтального стебля или корневища.
Хвощи и плауны	Биология.	Хвощи встречаются на всем земном шаре, кроме Австралии и Новой Зеландии, и насчитывают около 30 видов. Обитают преимущественно во влажных местах.
Отдел Голосеменные	Биология.	Семенные растения обладают тремя очень важными преимуществами: разноспоровостью, способностью к образованию семян, способностью продуцировать неподвижные мужские гаметы, вегетативное тело семенных растений образует споры двух типов: микроспоры (мужские) и мегаспора (женские).
Отдел Покрытосеменные, или цветковые растения	Биология.	Отличительной особенностью этого отдела является наличие плода, развивающегося из завязи цветка. Покрытосеменные представлены: деревьями, травами и промежуточными формами — кустарниками и кустарничками.
Цветковые растения. Класс однодольные	Биология.	Насчитывает около 4 тыс. видов. Жизненные формы: многолетние травы с корневищами, луковицами, клубнелуковицами, реже древовидные растения (алоэ, юкка, драцены). Листья очередные, с параллельным или дуговым жилкованием.
Цветковые растения. Класс двудольные	Биология.	Это многолетние и однолетние растения: капуста, редька, редис, сурепка, пастушья сумка и др. Листья крестоцветных расположены поочередно, нижние образуют прикорневую розетку. Соцветия верхушечные, кистевидные или щитковидные.
Царство Грибы	Биология.	Царство организмов, сочетающее признаки растений и животных. С животными их сближает гетеротрофный способ питания, наличие хитина в составе клеточной стенки, образование мочевины в процессе обмена веществ, гликогена в качестве запасного питательного вещества.
Общие сведения о животных. Одноклеточные	Биология.	Более 2 млн видов животных, обитающих повсеместно, отличаются от растений гетеротрофностью питания, подвижностью, развитой опорно-двигательной системой, сложностью поведенческих реакций.
Многоклеточные животные. Тип Кишечнополостные	Биология.	В отличие от клеток Простейших, способных самостоятельно выполнять все жизненно важные функции, клетки многоклеточных организмов выполняют одну определенную функцию.
Тип Плоские черви	Биология.	Плоские черви — трехслойные животные, у них появляется мезодерма, расположенная между эктодермой и энтодермой. Это свободноживущие и паразитические виды. Всего их насчитывается ок. 12 500 видов.
Тип Круглые черви	Биология.	К типу относятся несколько классов, в том числе самый многочисленный класс Нематоды, или собственно Круглые черви. Они обитают в морях, пресных водоемах, почве, в организмах животных, в тканях растений. Известно около 12 000 видов.
Тип Кольчатые черви	Биология.	Насчитывает около 7 000 видов. Это обитатели водоемов и почвы. Включает 3 класса.
Тип Моллюски	Биология.	Тип моллюски включает три класса: медленно ползающие улитки (брюхоногие), относительно оседлые двустворчатые и подвижные головоногие. Тип насчитывает около 130 000 видов.
Тип Членистоногие	Биология.	Членистоногие — самая большая группа животных, населяющая нашу планету. Его представители освоили все среды жизни: сушу, моря пресные водоемы, воздушное пространство. Их можно встретить во всех географических широтах.
Класс Насекомые	Биология.	К этому классу относятся наиболее высокоорганизованные членистоногие. Известно по разным данным 2-4 млн видов. Большинство насекомых обитает на суше, некоторые — в пресных водоемах.
Тип Хордовые	Биология.	Наименее организованный представитель хордовых — ланцетник, относится к очень древней группе бесчерепные. Он имеет признаки, сходные с беспозвоночными и позвоночными, ведет пассивный водный образ жизни.
Надкласс Рыбы	Биология.	Рыбы относятся к позвоночным животным. Для позвоночных характерно наличие черепа, позвоночника и парных конечностей (или плавников). Передний конец нервной трубки у них формирует головной мозг, он защищен черепом.
Класс Земноводные (Амфибии)	Биология.	Это водно-наземные животные. Они имеют две пары конечностей, состоящих из трех отделов.
Класс Пресмыкающиеся (Рептилии или Гады)	Биология.	Большинство рептилий — наземные животные, но некоторые виды обитают в воде (морские черепахи, змеи). Тело животных, как правило, разделено на голову, туловище и хвост и покрыто роговыми чешуйкам или щитками, защищающими их от механического воздействия и высыхания.
Класс Птицы (Пернатые)	Биология.	Птицы — высокоорганизованные позвоночные. Их тело покрыто перьями, передние конечности видоизменены в крылья. Имеют постоянную температуру тела, которая обеспечивается интенсивным обменом веществ.
Класс Млекопитающие (Звери)	Биология.	Млекопитающие — теплокровные позвоночные животные с развитым волосяным покровом и вскармливающие своих детенышей молоком. Сердце у них четырехкамерное, хорошо развита центральная нервная система.
Эволюция животного мира	Биология.	Под эволюцией понимают необратимое историческое развитие органического мира с постепенным его усложнением. Формы животных так же менялись на Земле, как формы растений и других организмов.
Общий обзор организма человека	Биология.	Анатомия, физиология и гигиена человека составляют основу современной медицины, педагогики, психологии. Развитие этих наук помогает разрабатывать эффективные методы профилактики и лечения заболеваний человека.
Опорно-двигательная система человека	Биология.	Опорно-двигательная система образована скелетом и мышцами. Скелет человека составляет основу тела, определяет его размеры и форму и совместно с мышцами образует полости, в которых располагаются внутренние органы.
Ткани, их строение и функции	Биология.	Эпителиальная ткань входит в состав покровов тела, полостей и желез, оболочек внутренних органов. Клетки эпителия расположены на базальной мембране и близко прилегают друг к другу, благодаря малому количеству межклеточного вещества.
Мышцы. Их строение и функции	Биология.	Скелетных мышц у взрослого человека насчитывается около 400. Все они состоят из поперечно-полосатой мышечной ткани.
Внутренняя среда организма	Биология.	У высших животных и человека внутренняя среда организма образована кровью, тканевой жидкостью и лимфой. Она характеризуется относительным постоянством состава, физических и химических свойств, т.е. гомеостазом.
Иммунитет	Биология.	Русский ученый И. И. Мечников установил, что лейкоциты играют решающую роль а защите организма от инфекционных болезней, уничтожая возбудителей путем их поглощения и переваривания.
Кровообращение. Лимфообращение	Биология.	Кровообращение — это движение крови по сосудам за счет сокращений сердца. Система органов кровообращения состоит из сердца и кровеносных сосудов (артерий, вен, капилляров), пронизывающих все органы и ткани тела.
Строение сердца	Биология.	Сердце человека представляет собой полый мышечный орган, разделенный на четыре камеры: два предсердия и два желудочка. Оно находится в левой половине грудной полости, на уровне 2-5 ребер и лежит в околосердечной сумке, образованной соединительной тканью.
Дыхание	Биология.	Дыхание — это совокупность процессов, обеспечивающих поступление в организм кислорода и удаление из него углекислого газа, образовавшегося в промессе биологического окисления.
Газообмен в легких и тканях	Биология.	Газообмен в легких происходит путем диффузии. Кислород через тонкие стенки альвеол и капилляров поступает из воздуха в кровь, а углекислый газ из крови в воздух. Диффузия газов происходит в результате разности их концентраций в крови и в воздухе.
Пищеварение	Биология.	Пищеварение — это процесс механической обработки пищи в пищеварительном канале, ее ферментативное расщепление на более простые питательные вещества, способные всасываться в кровь.
Размножение человека	Биология.	Человек, как и все живые организмы, способен к воспроизведению, т. е. к сохранению и продолжению своего вида. Размножение происходит половым способом, при котором половые клетки сливаются и образуют зиготу, дающую начало новому организму.
Выделение	Биология.	Образовавшиеся в процессе обмена веществ конечные продукты распада, являющиеся ядовитыми для организма, удаляются из него через почки, кожу, потовые железы, легкие и кишечник.
Кожа	Биология.	Кожа — наружный покров тела, который обеспечивает температурную, болевую, осязательную чувствительность, препятствует проникновению микробов и ядовитых веществ в организм, предохраняет его от механических повреждений.
Железы внутренней секреции	Биология.	Гуморальная регуляция функций оргат низма осуществляется с помощью химических веществ, вырабатываемых в различных органах и тканях, и кровью разносимых по всему организму.
Нервная система человека	Биология.	Нервная система обеспечивает постоянство внутренней среды организма. Кроме этого нервная система согласует работу всех органов, регулирует их деятельность, обеспечивает сокращение мышц.
Органы чувств (Анализаторы)	Биология.	Органы чувств обеспечивают восприятие различных раздражений, действующих на организм, и служат для приспособления к меняющимся условиям окружающей среды.
Высшая нервная деятельность	Биология.	В основе учения о высшей нервной деятельности лежат идеи о рефлекторных механизмах психических процессов, которые впервые сформулировал И.М. Сеченов.
Общие биологические закономерности	Биология.	Органический мир изменчив и непрерывно развивается со времени его возникновения в силу естественных материальных причин.
Основные положения клеточной теории, ее значение	Биология.	Все живые организмы состоят из клеток. Клетка — элементарная единица строения, функционирования и развития живых организмов. Существуют неклеточные формы жизни — вирусы, однако они проявляют свои свойства только в клетках живых организмов.
Химический состав клеток	Биология.	Клетка состоит из тех же химических элементов, что и неживая природа: в ней присутствует большинство элементов периодической системы Менделеева.
Обмен веществ и превращение энергии в клетке	Биология.	Обмен веществ и энергии (метаболизм) осуществляется на всех уровнях организма: клеточном, тканевом и организменном. Он обеспечивает постоянство внутренней среды организма — гомеостаз — в непрерывно меняющихся условиях существования.
Фотосинтез	Биология.	Фотосинтез — это процесс образования органических соединений из неорганических веществ с использованием энергии солнечного света. Его биологическое значение заключается в обеспечении живых организмов Земли органическими веществами, обогащении атмосферы Земли кислородом.
Синтез белка	Биология.	Синтез белка и фотосинтез относятся к реакциям пластического обмена. Синтез белков наиболее активно протекает в молодых растущих клетках. Основная роль в определении структуры белков принадлежит ДНК.
Вирусы, их строение и функционирование	Биология.	Вирусы — это неклеточныв формы жизни, различимые только под электронным микроскопом. Это внутриклеточные паразиты. За пределами клетки они не проявляют своих свойств и имеют кристаллическую форму.
Деление клеток — основа размножения и роста организмов	Биология.	Деление клеток — процесс, лежащий в основе размножения и индивидуального развития всех живых организмов. Основную роль в делении клеток играет ядро.
Мейоз	Биология.	Мейоз — особый вид деления клеток, в результате которого образуются гаметы — половые клетки с гаплоидным набором хромосом.
Половое и бесполое размножение организмов	Биология.	Размножение — это свойство живых организмов воспроизводить себе подобных, в основе которого лежит передача наследственной информации от родителей потомству.
Эмбриональное развитие животных	Биология.	Независимо от способа размножения, начало новому организму дает одна клетка, содержащая наследственные задатки и обладающая всеми характерными признаками и свойствами целого организма.
Основы генетики. Законы наследственности	Биология.	Генетика — наука, изучающая закономерности наследственности и изменчивости. Мендель, проводя опыты по скрещиванию различных сортов гороха, установил ряд законов наследования, положивших начало генетике.
Половые хромосомы и аутосомы. Генотип	Биология.	Аутосомы — парные хромосомы, одинаковые для мужских и женских организмов. В клетках тела человека 44 аутосомы (22 пары).
Изменчивость, ее формы и значение	Биология.	Изменчивость — это способность организма приобретать новые признаки в процессе онтогенеза. Различают наследственную и ненаследственную изменчивость.
Приспособленность организмов к среде обитания, ее причины	Биология.	Приспособленность — соответствие признаков организма (внутреннего и внешнего строения, физиологических процессов, поведения) среде обитания, позволяющее выжить и дать потомство.
Генетика и теория эволюции	Биология.	Мутации составляют основу наследственной изменчивости. Особи с различными мутациями, скрещиваясь между собой, обретают новые сочетания генов. Мутационная изменчивость дает первичный материал для естественного отбора, ведущего к образованию новых видов.
Додарвиновский период в развитии биологии	Биология.	С установлением христианского мировоззрения в Европе была распространена официальная точка зрения о возникновении живой природы: все живое создано богом и остается неизменным (креационизм).
Эволюционное учение Дарвина	Биология.	Ч. Дарвин доказал, что огромное многообразие видов, населяющих Землю, образовалось благодаря постоянно возникающим в природе разнонаправленным наследственным изменениям и естественному отбору.
Антропогенез	Биология.	На научную основу вопрос о происхожении человека впервые поставил Дарвин. В труде «Происхождение человека и половой отбор» (1871 г.) он показал, что человек имеет животное происхождение и характеризуется большим сходством с современными человекообразными обезьянами.
Основы селекции	Биология.	Одним из основоположников селекции является Ч. Дарвин, раскрывший роль наследственной изменчивости и искусственного отбора в создании новых пород и сортов.
Основы экологии. Биогеоценоз	Биология.	Биогеоценоз (экосистема) — совокупность, взаимосвязанных между собой популяций разных видов, длительно обитающих на определенной территории с относительно одинаковыми условиями.
Агроценоз	Биология.	Агроценоз — искусственный биогеоценоз, появившийся в результате сельскохозяйственной деятельности человека. Примеры: сад, пастбище, поле.
Учение о биосфере	Биология.	Термин «биосфера» предложен в 1875г. австрийским геологом Э. Зюссом. В начале XX в. В.И. Вернадский разработал учение о биосфере. Согласно Вернадскому, биосфера — оболочка Земли, населенная живыми организмами, активно ими преобразуемая.

Шпаргалки (шпора) по Географии.

География:
Государственные границы. Режим территории	География.	Политическая карта мира отражает место стран в современном мире, размеры их территории, форму правления и государственного устройства, границы и т. п.
Суверенные государства и несамоуправляющиеся территории	География.	Главными объектами политической карты являются суверенные государства и несамоуправляющиеся территории. Если в 1900 г. на Земном шаре было всего 55 суверенных государств, то к 2002 г. суверенитетом обладало уже более 190 стран.
Новейший этап формирования политической карты мира	География.	Процесс формирования политической карты мира насчитывает несколько тысячелетий, поэтому можно говорить о существовании нескольких периодов в ее формировании.
Формы правления и государственные устройства	География.	Республиканская форма правления возникла в древности, но наибольшее распространение она получила в периоды Новой и Новейшей истории. В 1991 г. в мире было 127 республик, но после распада СССР и Югославии их общее число превысило 140.
Типология стран мира	География.	В настоящее время с учетом уровня и характера социально-экономического и политического развития, выделяют три группы стран мира.
Многообразие стран современного мира	География.	В настоящее время на политической карте выделяется около 230 стран и территорий. Более 190 из них являются суверенными, т.е. политически независимыми государствами, обладающими самостоятельностью во внутренних и внешних делах.
Основные формы государственно-территориального устройства	География.	В мире существует две основные формы государственного правления: республиканская и монархическая. Республика — форма правления, при которой все высшие органы власти либо избираются, либо создаются парламентами — общенациональными представительными учреждениями.
Природные ресурсы земного шара:
Географическая среда и ее роль в жизни человека	География.	Географической средой называется та часть земной природы, с которой человеческое общество непосредственно взаимодействует в своей жизни и производственной деятельности на данном этапе исторического развития.
Виды природных ресурсов. Ресурсообеспеченность	География.	Природные ресурсы — это естественные ресурсы или природные вещества и виды энергии, служащие средствами существования человеческого общества и используемые в хозяйстве.
Природопользование	География.	Под природопользованием понимают деятельность человеческого общества, направленную на удовлетворение своих потребностей путем использования природных ресурсов. Выделяют рациональное и нерациональное природопользование.
Загрязнение окружающей среды и экологические проблемы человечества	География.	Под загрязнением окружающей среды понимают нежелательное изменение ее свойств в результате антропогенного поступления различных веществ и соединений.
Минеральные ресурсы	География.	Потребности в минеральном сырье, составляющем базу для производства промышленной продукции, возрастают из года в год. Ежегодно в мире из недр извлекается более 100 млрд т различного минерального сырья и топлива.
Виды минеральных ресурсов	География.	Минеральными ресурсами называются полезные , ископаемые, извлеченные из недр.
Земельные и лесные ресурсы	География.	Земельные ресурсы и почвенный покров Земли — основа живой природы и с/х производства. Мировой земельный фонд составляет 13 млрд га, в том числе обрабатываемые земли — 11 %, луга и пастбища — 23 %, остальное — леса, кустарники и неудобья.
Обеспеченность земельными ресурсами	География.	Земельные ресурсы — это земная поверхность, пригодная для проживания человека, для строительства и любых других видов хозяйственной деятельности.
Водные ресурсы	География.	Жизнь и хозяйственная деятельность человека связаны, прежде всего, с пресными водами, которые используются в быту, для нужд промышленности и сельского хозяйства.
Водные ресурсы суши	География.	Существует несколько направлений использования водных ресурсов. Наиболее важным из них является удовлетворение потребностей человечества в пресной воде. Для этого широко используются речные воды.
Лесные ресурсы мира	География.	Лесные ресурсы — важнейший вид ресурсов биосферы. В лесные ресурсы входят: древесина, живица, пробка, грибы, плоды, ягоды, орехи, лекарственные растения, охотничье-промысловые ресурсы и т.д.
Ресурсы Мирового океана	География.	Основными ресурсами Мирового океана считаются биологические, минеральные и энергетические. Их изучением занимались крупнейшие отечественные исследователи, такие как: Ю.М.Шокальский. В.Ю. Визе, Н.Н. Зубов, П.П.Ширшов, К.К.Марков и др.
Природно-рекреационные ресурсы их виды	География.	Природно-рекреационные ресурсы — объекты и явления природы, которые можно использовать в целях отдыха, туризма и лечения. Как видно из определения, этот вид ресурсов выделяется не по особенностям происхождения, а по характеру использования.
Численность и динамика населения	География.	В октябре 1999г., по оценкам специалистов ООН, население планеты достигло уже 6 млрд человек. Численность населения мира росла особенно быстро в XX в. Это хорошо видно из сопоставления сроков миллиардных приростов человечества.
Численность населения мира и ее изменения	География.	Данный вопрос является предметом изучения демографии — науки о закономерностях воспроизводства населения, его численности, естественном приросте, возрастном и половом составе и т. д.
Типы и режимы воспроизводства населения	География.	В соответствии с изменением совокупности демографических показателей принято выделять три основных исторических типа воспроизводства населения. Первый и самый ранний из них— так называемый архетип воспроизводства населения.
Половозрастная структура населения мира	География.	Возрастная структура населения соответствует его распределению по возрастным группам. Обычно в демографии используются одногодичные, пятилетние или десятилетние возрастные группы.
«Демографический взрыв»	География.	Феномен быстрого роста населения в странах второго типа воспроизводства населения (с высокими и очень высокими показателями рождаемости и естественного прироста и относительно низкими показателями смертности) получил название «Демографического взрыва».
Миграции населения	География.	В условиях глобального снижения интенсивности естественного движения населения все большее влияние на размещение человечества оказывают миграции — трансграничные перемещения населения, связанные с долговременной или окончательной переменой места жительства.
Примеры внутренних и внешних миграций	География.	Миграции (от латинского «migratio») — перемещения людей между отдельными территориями и поселениями, связанные с постоянной, временной или сезонной переменой ими места жительства.
Трудовые ресурсы и их использование	География.	Понятие «трудовые ресурсы» объединяет всех людей, находящихся в трудоспособном возрасте (за вычетом инвалидов и других людей, неспособных к труду), и работающих людей старше и младше трудоспособного возраста.
Национальный состав населения мира	География.	Национальный состав населения — распределение людей по признаку этнической принадлежности. Этнос (или народ) — это исторически сложившаяся устойчивая общность людей, объединенная единством языка, территории, хозяйственной жизни и культуры, национальным самосознанием.
Религиозный состав населения	География.	Религии делятся на примитивные, национальные (местные) и мировые. Примитивные или «языческие» верования (магия, тотемизм, фетишизм, анимизм, шаманизм и др.) типичны для родо-племенных обществ.
Расселение населения мира	География.	Расселение населения — это процесс распределения населения по территории и формирование сети поселений.
Размещения населения	География.	Размещение населения отражает результат процесса расселения населения на конкретный период времени. Расселены люди на планете крайне неравномерно.
Факторы, влияющие на размещение населения	География.	Анализ размещения населения — важная задача географии населения. Чаще всего оно определяется количеством жителей на 1 квадратный километр, то есть показателями плотности населения (по миру он составляет 40 человек на квадратный километр).
Урбанизация, важнейшие агломерации	География.	Размещение по регионам мира сельского и городского населения заметно отличается от «усредненной» картины.
Соотношение городского и сельского населения	География.	Соотношение городского и сельского населения на протяжении человеческой истории претерпело значительные изменения. Большие различия наблюдались также между отдельными регионами мира.
Национальный состав населения мира	География.	Население земного шара состоит из большого количества (3-4 тыс.) так называемых этнических общностей.
Возрастной и половой состав населения мира	География.	Особенности естественного движения, как и миграции, определяют возрастную и половую структуру населения.
География мирового хозяйства:
Понятие о мировом хозяйстве	География.	Основу мирового хозяйства составляет разнообразная деятельность людей, обеспечивающая получение различных видов продукции в промышленном производстве и сельском хозяйстве, а также многие виды услуг в сфере производства.
Сущность и основные этапы формирования мирового хозяйства	География.	Мировое хозяйство (М. к.) — исторически сложившаяся совокупность национальных хозяйств всех стран мира, связанных между собой всемирными экономическими отношениями.
Состав и структура мирового хозяйства	География.	Отраслевая структура хозяйства — совокупность его частей (отраслей и подотраслей), исторически сложившаяся в результате общественного разделения труда.
Международная экономическая интеграция	География.	Международная экономическая интеграция (МЭИ) — одно из ярких проявлений интернационализации хозяйственной жизни в эпоху НТР.
Международное географическое разделение труда. Интеграционные группировки	География.	Международное разделение труда представляет собой специализацию отдельных стран на производстве и обмене теми или иными товарами и услугами. При этом экономика каждой страны становится как бы частью мирового производства.
Факторы размещения производительных сил и их изменения в эпоху НТР	География.	Факторами размещения принято считать совокупность условий для наиболее рационального выбора места размещения хозяйственного объекта, группы объектов, отрасли или же конкретной территориальной организации структуры хозяйства.
Тенденции изменения отраслевой структуры мирового хозяйства	География.	Хозяйство отдельных стран и мира в целом состоит из отдельных отраслей, исторически возникших в результате общественного разделения труда.
Научно-техническая революция: характерные черты и составные части	География.	Развитие человеческой цивилизации связано с научно-техническим прогрессом. На фоне этого прогресса выделяются отдельные периоды быстрого и глубокого изменения производительных сил, в процессе которых происходит качественный переворот в этих силах.
Добывающая и обрабатывающая промышленность	География.	Промышленность (индустрия) имеет самую развитую и разветвленную структуру среди всех отраслей хозяйства. Она состоит из многих производств, очень сильно отличающихся друг от друга.
Машиностроение	География.	Машиностроение лидирует по стоимости продукции в развитых странах: на отрасль приходится до 35—40 % всей стоимости промышленной продукции и до 1/3 всех работающих в индустрии.
Машиностроительный комплекс	География.	Машиностроительный комплекс — совокупность отраслей промышленности, производящих оборудование для всех подразделений хозяйства, а также многие предметы потребления.
Химическая промышленность	География.	Химическая промышленность, как и машиностроение, — одна из самых сложных по своей структуре отраслей.
Значение химической промышленности	География.	Химическая промышленность — одна из авангардных отраслей научно-технической революции, наряду с машиностроением, это самая динамичная отрасль современной индустрии.
Топливно-энергетический комплекс	География.	Энергетика — одна из базовых отраслей тяжелой промышленности. Это самая ма-териалоемкая отрасль мировой индустрии: ежегодно общее количество добытых и использованных ею видов топлива достигает 12-13 млрд т.
Электроэнергетика	География.	Доля электроэнергетики в структуре потребления энергии составляет более 1/3, предполагается, что к концу XX века эта доля может подняться до ½. Но после энергетического кризиса 70-х годов и этот сектор мировой энергетики несколько замедлил свое развитие.
Пути решения энергетической проблемы	География.	Топливно-энергетическая промышленность включает топливную отрасль (т.е. добычу и переработку различных видов топлива) и электроэнергетику.
Главные районы добычи топлива	География.	На современном этапе это ведущая отрасль мировой топливно-энергетической промышленности. Географическое распределение запасов нефти: Доля развивающихся стран в этих запасах — 86%. Наиболее крупные нефтяные районы — регион Персидского залива, Россия, Мексиканский залив, карибский бассейн.
Металлургическая промышленность	География.	Металлургическая промышленность — отрасль тяжелой промышленности, производящая разнообразные металлы. Она включает две отрасли: черную и цветную металлургию.
Черная металлургия	География.	Железо (чугун, сталь, прокат) было и остается самым массовым конструкционным материалом в мировом хозяйстве. Основная область применения черных металлов — машиностроение, растет его значение в строительстве.
Цветная металлургия	География.	Области применения цветных металлов быстро расширяются, особенно в новейших отраслях машиностроения: в начале XX в. получали всего лишь 15 видов цветных металлов, а в настоящее время — более 70.
Пищевая промышленность	География.	Разнообразные производства пищевой промышленности призваны удовлетворять потребности населения в ряде важнейших продуктов питания. Отрасль очень специфична для отдельных регионов и стран, и даже в пределах последних.
Легкая промышленность	География.	Структура отрасли достаточно сложна. В нее входят сырьевые производства (получение хлопка из хлопка-сырца, обработка шкур животных), полупродуктовые (прядильное, текстильное, красильное, кожевенное, меховое), конечные пр-ва (швейное, трикотажное, ковровое, галантерейное, обувное и др.).
Легкая промышленность: состав, особенности, размещения	География.	Легкая промышленность включает в себя около 30 крупных отраслей. Географические проблемы развития легкой промышленности связаны с некоторыми ее особенностями.
Лесная и деревообрабатывающая промышленность	География.	Лесная промышленность — старейшая среди отраслей, производящих конструкционные материалы. Она объединяет предприятия лесозаготовительной, деревообрабатывающей, целлюлозно- бумажной и лесохимической промышленности.
Сельское хозяйство	География.	В животноводство входят много подотраслей, но основные — выращивание крупного рогатого скота, свиноводство, овцеводство, птицеводство.
География мирового сельского хозяйства	География.	Сельское хозяйство — старейшая отрасль материального производства. В 2001 г. в сельском хозяйстве было занято 1,3 млрд чел., а вместе с членами крестьянских семей — 2,6 млрд чел.
Животноводство	География.	Подобно зерновым культурам, животноводство распространено почти повсеместно, причем в структуре угодий луга и пастбища занимают в три раза больше земель, чем пашня. Основную часть животноводческой продукции дают страны умеренного пояса.
География животноводства	География.	Животноводство, как и растениеводство, относится к древнейшим отраслям экономики и имеет самое широкое территориальное распространение.
Растениеводство	География.	Большую часть (70%) потребляемого современным миром продовольствия обеспечивает растениеводство.
География растениеводства	География.	Характерная черта сельского хозяйства состоит в том, что его производственные процессы определяются биологическими законами. В настоящее время с/х производство сконцентрировано в умеренном и жарком поясе.
Типы сельского хозяйства	География.	При генерализованном подходе выделяют 3 основные социально-производственные категории сельского хозяйства, каждая из которых объединяет несколько типов.
География мирового транспорта	География.	Транспорт — одна из важнейших отраслей экономики любой страны. Это важная система в сложном механизме мирового хозяйства, которая обеспечивает производственные связи, осуществляет перевозки грузов и пассажиров.
Значение транспорта в мировом хозяйстве	География.	Транспорт — одна из важнейших отраслей хозяйства. Он обеспечивает производственные связи промышленности и сельского хозяйства, осуществляет перевозки грузов и пассажиров, является основной географического развития труда.
География мировых экономических связей	География.	Анализ международных экономических связей ставит своей целью выявление особенностей и закономерностей обмена специализированными видами товаров и услуг, изменения структуры мирового экспорта и импорта.
Мировая торговля услугами	География.	Международная торговля услугами становится все более важным и быстро растущим сегментом мировых экономических связей. Основными их видами являются экспорт и импорт транспортных и туристических услуг, банковские, страховые, информационные, образовательные, медицинские, консультационные услуги и т. д.
Экономическая и социальная география регионов и стран:
Международные экономические отношения	География.	К международным экономическим отношениям (МЭО) можно отнести мировую (международную) торговлю, международные кредитно-финансовые отношения, международное производственное сотрудничество, международные научно-технические связи, предоставление международных услуг.
Общая экономико-географическая характеристика стран Западной Европы	География.	Западная Европа — субрегион зарубежной Европы, включающий 26 государств, сильно отличающихся друг от друга по величине, государственному устройству и уровню социально-экономического развития.
Общая экономико-географическая характеристика ФРГ	География.	ФРГ — государство в Центральной Европе. Оно граничите Нидерландами, Бельгией, Люксембургом, Францией, Швейцарией, Австрией, Чехией, Польшей, Данией.
Общая экономико-географическая характеристика стран Восточной Европы	География.	Восточная Европа как историко-географический регион включает: Польшу, Чехию, Словакию, Венгрию, Румынию, Болгарию, страны, образовавшиеся в результате распада бывшей Югославии (Словению, Хорватию, Сербию, Боснию, Герцеговину, Черногорию, Македонию), Албанию, Латвию, Литву, Эстонию.
Общая экономико-географическая характеристика одной из стран Восточной Европы. Венгрия	География.	Венгрия — государство в Восточной Европе, расположенное на Среднедунайской низменности. Венгрия — президентская республика. В течение многих лет активно участвовала в СЭВ.
Общая экономико-географическая характеристика США	География.	США — наиболее экономически развитое государство Запада. По площади США превосходят всю Европу, но уступают России. Страна состоит из 50 штатов и федерального округа Колумбия.
Общая экономико-географическая характеристика Японии	География.	Япония — страна — архипелаг, расположенная на четырех крупных и почти четырех тысячах мелких островов, вытянувшихся дугой в 3,5 тыс. км. с северо-востока на юго-запад вдоль восточного побережья Азии.
Общая экономико-географическая характеристика Китайской народной республики	География.	КНР — третье по территории государство мира и первое по численности населения — расположено в центральной и восточной Азии. Государство граничит с 16 странами, 1/3 границ приходится на страны СНГ.
Общая экономико-географическая характеристика стран Латинской Америки	География.	Латинской Америкой (Л.А.) называют регион Западного полушария, расположенный между США и Антарктидой. В составе Л.А. выделяют несколько субрегионов.
Общая экономико-географическая характеристика одной из стран Латинской Америки. Бразилия	География.	Бразилия — самое крупное государство Южной Америки, расположено в ее центральной и восточной частях. Длина сухопутных границ — около 16 тыс. км., на востоке на протяжении 7,4 тыс. км. страна омывается Атлантикой.
Общая экономико-географическая характеристика стран Африки	География.	Материк занимает 1 /5 суши земного шара. По размерам (30,3 млн. км2 — с островами) из всех частей света уступает только Азии. В состав региона входят 55 стран. Существуют несколько вариантов деления Африки на регионы.
Общая экономико-географическая характеристика одной из стран Африки. ЮАР	География.	ЮАР — единственное в Африке высокоразвитое государство. По всем показателям экономического развития ей принадлежит первое место в Африке.
Общая экономико-географическая характеристика Азии	География.	Зарубежная Азия — самый крупный по площади и населению регион мира, причем это первенство он сохраняет, по существу, на протяжении всего существования человеческой цивилизации.
Общая экономико-географическая характеристика одной из стран Азии. Индия	География.	Республика Индия расположена в Южной Азии на полуострове Индостан. В ее состав также входят Лаккадивские острова в Аравийском море, Андаманские и Никобарские в Бенгальском заливе.
Глобальные проблемы человечества:
Причины возникновения глобальных проблем	География.	В силу ряда причин такие проблемы, как предотвращение мирового ядерного конфликта, мировых и локальных войн, сохранение природной среды, надежное обеспечение человечества энергией.
Экологический кризис	География.	На протяжении столетий человек бесконтрольно брал все, что дает ему природа. Научные достижения создали иллюзию почти полной управляемости миром. Природа испытывает влияние общества по многим направлениям.
Демографическая проблема	География.	В настоящее время на планете проживает более 6 млрд человек. Население растет очень быстро, ежесекундно увеличиваясь на 3 человека.
Продовольственная проблема	География.	Дефицит продуктов сопровождал человечество на всем протяжении его развития. В связи с развитием мировой торговли и транспорта эта проблема несколько ослабла, но не исчезла.
Ресурсная проблема	География.	Развитие человеческого общества во все века было связано с использованием разнообразных ресурсов. Природная среда является местом обитания человека и источником всех благ, необходимых для его жизни и производственной деятельности.
География России:
Геополитическое положение и административно-политическое устройство России	География.	Россия (Российская Федерация)— самое большое по территории государство мира. Площадь его равна 17,1 млн км2, что составляет более 1/9 площади суши.
Особенности географического положения России	География.	Россия является крупнейшей страной мира (1/8 часть суши). Площадь России— 17,1 млн. км2, что почти в два раза больше, чем КНР или США. Российская территория сопоставима с целым материком — Южной Америкой.
Часовые пояса на территории России	География.	Земля совершает полный оборот (360°) за сутки (24 часа). В разных точках Земли, расположенных на разных'меридианах, т.е. имеющих разную долготу, в один и тот же момент часы показывают разное время суток.
Изменения в геополитическом положении России	География.	Распад Советского Союза имел для России целый ряд важных последствий. Прежде всего, это изменение геополитического и социально-экономического положения страны.
Государственный строй и административно-территориальное деление России	География.	Российская Федерация (Россия) — суверенная демократическая республика имеет федеративную форму государственного устройства.
Природные условия и природные ресурсы:
Рельеф и геологическое строение	География.	Рельеф — совокупность неровностей земной поверхности. Эти неровности называют формами рельефа. Рельеф сформировался в результате взаимодействия внутренних (эндогенных) и внешних (экзогенных) геологических процессов.
Минеральные ресурсы России	География.	Природные ресурсы — компоненты природы, которые непосредственно участвуют (или могут быть использованы) в материальном производстве и непроизводственной деятельности.
Климат России	География.	Россию пересекают четыре климатических пояса: арктический, субарктический, умеренный и субтропический. Положение преимущественно в высоких и средних широтах определяет существование на большей части территории сурового климата.
Агроклиматические ресурсы России	География.	Агроклиматические ресурсы России создают возможность для разностороннего развития сельского хозяйства.
Внутренние воды России	География.	Внутренние воды составляют многочисленные реки, озера, болота, подземные воды, ледники, искусственные водоемы, водохранилища, пруды, каналы.
Водные и гидроэнергетические ресурсы России	География.	Водные ресурсы России значительны и разнообразны. Запасы пресной воды содержатся не только в реках, озерах, водохранилищах, но также и в подземных водоемах, педниках, многопетней мерзлоте и болотах.
Почвы и земельные ресурсы России	География.	Размещение основных типов почв на поверхности Земли подчинено закону географической зональности, как установил около 100 лет назад В.В.Докучаев.
Лесные ресурсы России	География.	Лесные ресурсы имеют многоцелевое назначение. С одной стороны, это ценное промышленное сырье, с другой — топливо. Велика роль леса в сохранении определенного климата, поддержании водного режима, очистке воздушного бассейна.
Экологические проблемы в России	География.	Экологическая ситуация в России продолжает оставаться тревожной. Отрасли добывающей промышленности создают специфические промышленные ландшафты с карьерами, шахтами, отвалами пустой породы.
Население России:
Динамика численности и воспроизводство населения	География.	По числу жителей Российская Федерация находится на 7-м месте в мире после Китая, Индии, США, Индонезии, Бразилии, Пакистана. Но в отличие от этих стран, численность населения нашей страны последние десять лет постепенно уменьшается.
Миграции населения	География.	Миграции населения — это перемещения людей из одного постоянного места жительства в другое на более или менее длительное время.
Переселение	География.	Миграции (от лат. migratio) — переселение, перемещение людей. Необходимо, прежде всего, различать внутренние и внешние виды миграции.
Городское и сельское население	География.	В России существуют два основных типа поселений — городские и сельские населенные пункты.
Размещение населения	География.	Распределение населения по территории и его пространственную организацию называют расселением. Расселение есть результат развития хозяйства, которое, в свою очередь, ориентируется на сложившуюся систему расселения.
Заселение территории России	География.	История заселения и освоения земель, различия в типах воспроизводства населения, обширность территории и разнообразие природных условий обусловили очень неравномерное распределение населения России.
Национальный состав населения	География.	Россия — многонациональное государство. Характеристика этнического состава проводится по результатам переписи населения.
Национальный и религиозный состав населения	География.	В России проживает более 100 народов и народностей, принадлежащих в основном к четырем языковым семьям: индоевропейской (87 % населения), алтайской (8 %), уральской (2 %) и северокавказской (2 %).
Численность населения России и ее изменения. Естественный прирост	География.	По численности населения (145,6 млн. чел. в 2000 г.) Россия находится на седьмом месте после Китая, Индии, США, Индонезии Бразилии, Пакистана.
Культурно-исторические особенности народов России. Основные религии, распространенные в стране	География.	Россия — огромная многонациональная страна. Каждый из населяющих ее народов характеризуется культурными, религиозными и бытовыми особенностями. Эти особенности являются результатом многовековой истории развития каждого народа.
География хозяйства России:
Современная экономика России	География.	В настоящее время весь хозяйственный комплекс страны переживает острый кризис. Негативные явления накапливались в течение многих десятилетий.
Отраслевая и территориальная структура хозяйства России	География.	Хозяйство страны представляет собой совокупность отраслей материальной и нематериальной сфер производства.
Отраслевой состав и межотраслевые комплексы	География.	В экономике страны выделяют ряд секторов, объединяющих несколько отраслей по функциональным особенностям использования ресурсов и производства необходимой продукции.
Топливно-энергетический комплекс	География.	Топливно-энергетический комплекс (ТЭК) — сложная межотраслевая система добычи и производства топлива и энергии, их транспортировки, распределения и использования.
Отраслевой состав и межотраслевые комплексы	География.	В экономике страны выделяют ряд секторов, объединяющих несколько отраслей по функциональным особенностям использования ресурсов и производства необходимой продукции.
Топливно-энергетический комплекс. Газовая область	География.	Топливно-энергетический комплекс (ТЭК) — совокупность отраслей по добыче и производству топлива и энергии, а также транспортировке и распределению этих продуктов.
Угольная промышленность и электроэнергетика	География.	По качеству (теплотворности) различают уголь бурый и каменный, в том числе коксующийся. Последний используется в черной металлургии, т.к. способен при высоких температурах спекаться, образуя необходимый компонент (кокс) для выплавки чугуна.
Электроэнергетика	География.	Электроэнергетика объединяет все процессы производства, передачи, трансформации и потребления электроэнергии. Она решающим образом влияет на уровень развития НТП в стране, а также на территориальную организацию народного хозяйства.
Нефтяная промышленность	География.	До середины 1950-х гг. были основными районами добычи нефти были Азербайджан и Сев. Кавказ. Затем лидерство перешло к Волго-Уральской провинции. Начиная с 1960-х гг. широко вовлекаются в разработку ресурсы Западной Сибири.
Металлургический комплекс	География.	Металлургический комплекс — совокупность отраслей, производящих разнообразные металлы. Подразделяется на черную и цветную металлургию. 90 процентов металлов, применяемых в современном производстве, — черные, т.е. железо и полученные на его основе сплавы.
Комплекс отраслей по производству конструкционных материалов. Черная металлургия	География.	В этот комплекс входят черная и цветная металлургия, химическая промышленность, лесопереработка и целлюлозно-бумажная промышленность.
Цветная металлургия	География.	Отрасль включает в себя добычу и обогащение руды, выплавку металлов, производство проката. К цветной металлургии относится и добыча алмазов. В последние годы производство основных цветных металлов существенно снизилось, а большая их часть стала отправляться за рубеж.
Химическая промышленность	География.	Химико-лесной комплекс имеет огромное значение для хозяйства России. Он объединяет технологически взаимосвязанные предприятия лесной и химической промышленности. Отрасли комплекса тесно связаны со всеми другими отраслями.
Лесная промышленность	География.	Включает заготовку, механическую обработку и химическую переработку древесины. Промышленность развивается на основе огромных массивов российских лесов.
Химико-лесной комплекс	География.	В отрасли выделяют три крупных блока: горная химия (добыча апатитов и фосфоритов для производства удобрений, поваренной и калийной солей, серы), основная химия (выпуск удобрений, соды, серной кислоты), производство полимерных материалов.
Машиностроительный комплекс	География.	Машиностроение — ведущий МОК нашей страны. Он состоит из большого числа подотраслей и производств, выпускающих разнообразные машины. Машиностроительный комплекс — основа научно-технического прогресса в российской экономике.
Машиностроение	География.	Машиностроение — это совокупность отраслей, производящих машины и осуществляющих обработку металла для производства машин (создание металлических конструкций и изделий).
Военно-промышленный комплекс	География.	ВПК — система отраслей, призванная обеспечить обороноспособность и независимость страны. Развал СССР и последовавший за этим экономический кризис нанесли значительный урон всему оборонному комплексу.
Агропромышленный комплекс	География.	Агропромышленный комплекс (АПК) — совокупность отраслей хозяйственного комплекса страны, обеспечивающих население продовольствием, а промышленность натуральным сырьем.
Развитие агропромышленного комплекса	География.	Агропромышленный комплекс (АПК) — комплекс отраслей промышленности и сельского хозяйства, принимающих участие в производстве и переработке сельскохозяйственной продукции.
Растениеводство и животноводство	География.	Растениеводство включает в себя полеводство, овощеводство, плодоводство, виноградарство, кормопроизводство и др. отрасли. Иногда как синоним применяют понятие «земледелие».
Растениеводство	География.	К этой отрасли относятся возделывание зерновых, зернобобовых культур, кормовых культур, овощей, бахчевых, картофеля, а также технических культур и многолетних насаждений.
Животноводство	География.	Животноводство дает 60% валовой продукции, доля его в составе АПК растет. Производство животноводческой продукции невозможно без прочной кормовой базы.
Транспортный комплекс	География.	Транспорт является одной из ведущих отраслей хозяйственного комплекса страны. Он осуществляет транспортировку уже созданного материального богатства или же людей.
Легкая промышленность	География.	Легкая промышленность включает почти два десятка отраслей, большинство из которых ориентируются на потребителя.
Развитие легкой промышленности	География.	Объединяет группу отраслей (их около 30), обеспечивающих население тканями, одеждой, обувью и другими предметами потребления. Легкая промышленность тесно связана с сельским хозяйством, особенно на стадии первичной переработки сырья.
Пищевая промышленность	География.	Пищевая промышленность производит продукты питания для людей. Она больше, чем другие отрасли, связана с сельским хозяйством, так как получает от него сырье.
Транспорт России	География.	Транспорт — «кровеносная система экономики». Развитие транспорта является непременным условием для функционирования хозяйства, жизни населения.
Внешние экономические связи России	География.	Внешние экономические связи являются результатом международного разделения труда, которое в свою очередь является частью территориального разделение труда (ТРТ).
Международные экономические связи России	География.	Современное мировое хозяйство характеризуется быстрым ростом внешнеэкономических связей. Участию в этих связях бывшего СССР препятствовали создавшаяся в мире ситуация противоборства Запада и Востока и «железный занавес».
Экономические районы России:
Территориальное разделение труда. Экономическое районирование	География.	Районирование— важнейший метод географической науки. Применение этого метода позволяет характеризовать крупные районы страны по специализации, участию в территориальном разделении труда.
Экономическое регионирование территории России	География.	Россия — огромная многоликая страна. Невозможно понять ее особенности и проблемы, не изучая внутреннее территориальное разнообразие.
Федеральные округа России	География.	Указом Президента Российской Федерации в мае 2000 г. установлена новая территориальная схема районирования страны, включающая 7 федеральных округов.
Западная экономическая зона России	География.	В составе Западной экономической зоны 8 экономических районов: Северный, Северо-Западный, Центральный, Центрально-Черноземный, Волго-Вятский, Северо-Кавказский, Поволжский, Уральский.
Западный макрорегион	География.	В состав Западного макрорегиона входят экономические районы европейской части России. Эту территорию можно назвать колыбелью Русского государства.
Центрально-Черноземный экономический район	География.	Состав района: (5 субъектов): Курская, Белгородская, Воронежская, Липецкая, Тамбовская обл. Площадь — 167,7 тыс. км2, население — 7,7 млн чел. (5,3 % от РФ).
Развитие Центрально-Черноземного экономического района	География.	Состав: Белгородская, Воронежская, Курская, Липецкая, Тамбовская области. Площадь-167 тыс. км2.
Центральный экономический район	География.	Состав района: (13 субъектов федера ции) — г. Москва, Московская, Ярославская Костромская, Ивановская, Владимирская Рязанская, Тульская, Орловская, Брянская Калужская, Смоленская, Тверская области.
Развитие Центрального экономического района	География.	Состав: Брянская, Владимирская, Ивановская, Калужская, Костромская, Орловская, Московская, Рязанская, Смоленская, Тверская. Тульская, Ярославская области, а также город федерального значения — Москва.
Волго-Вятский экономический район	География.	Состав района: (5 субъектов федерации) — Республика Марий Эл, Республика Мордовия, Чувашская Республика, Нижегородская обл., Кировская обл.
Развитие Волго-Вятского экономического района	География.	Состав: Кировская и Нижегородская области, Республики Марий Эл, Мордовская и Чувашская. Площадь — 265,4 тыс. км2. Население — 8 млн. 300 тыс. чел.
Северо-Западный экономический район	География.	Состав района: (4 субъекта федерации) — г. Санкт-Петербург, Ленинградская обл., Новгородская обл., Псковская обл.
Развитие Северо-Западного экономического района	География.	Состав: Ленинградская, Псковская и Новгородская области, город федерального значения Санкт-Петербург.
Калининградская область	География.	Особое место на северо-западе Российской Федерации занимает Калининградская область, образованная в 1946 г. Это исконно славяно-литовская земля, захваченная в 13 в. тевтонским орденом., истребившим здесь большую часть коренных жителей.
Северный экономический район	География.	Состав района: (6 субъектов федерации) — Республика Карелия, Республика Коми, Мурманская обл... Архангельская обл., Вологодская обл., Ненецкий АО.
Развитие Северного экономического района	География.	Состав: Архангельская, Вологодская. Мурманская области, республики Карелия и Коми, Ненецкий автономный округ.
Северо-Кавказский экономический район	География.	Состав района: (10 субъектов федерации) — Республика Адыгея, Карачаево-Черкесская Республика, Кабардино-Балкарская Республика, Республика Северная Осетия-Алания, Республика Ингушетия, Чеченская Республика, Республика Дагестан, Краснодарский край, Ставропольский край, Ростовская обл.
Развитие Северо-Кавказского экономического района	География.	Состав: Краснодарский край. Ставропольский край, Ростовская область и Республики: Адыгея, Дагестан. Ингушетия, Кабардино-Балкария, Карачаево-Черкессия, Северная Осетия-Алания, Чеченская.
Поволжье	География.	Состав: Астраханская, Волгоградская, Пензенская, Самарская, Саратовская, Ульяновская области. Республики: Калмыкия и Татарстан.
Поволжский экономический район	География.	Состав района: (8 субъектов федерации) — Республика Татарстан, Республика Калмыкия, Ульяновская обл., Пензенская обл., Самарская обл., Саратовская обл... Волгоградская обл., Астраханская обл.
Уральский экономический район	География.	Состав района: (8 субъектов федерации)— Республика Башкортостан, Удмуртская Республика, Пермская обл., Свердловская обл., Челябинская обл., Курганская обл., Оренбургская обл., Коми-Пермяцкий АО.
Развитие Уральского экономического района	География.	Состав: Курганская, Оренбургская, Пермская, Свердловская, Челябинская области. Республика Башкортостан, Республика Удмуртия, Коми-Пермяцкий автономный округ.
Восточный макрорегион	География.	Восточный макрорегион — крупнейшая по площади часть России (12,8 млн. км2) — 75% территории страны. К планетарной зоне Севера относится ½ территории Западной Сибири, 2/3 Восточной Сибири, ¾ Дальнего Востока, поэтому освоение региона связано с большими затратами; здесь проживает всего 22% населения страны.
Восточная экономическая зона России	География.	Восточная экономическая зона, или Восточный макрорегион состоит из трех самых больших по территории экономических районов России: Западно-Сибирского, Восточно-Сибирского, Дальневосточного.
Западно-Сибирский экономический район	География.	Состав района: (9 субъектов федерации)— Республика Алтай, Алтайский край, Кемеровская обл., Новосибирская обл., Омская обл., Томская обл., Тюменская обл., Ханты-Мансийский АО, Ямало-Ненецкий АО.
Развитие Западно-Сибирского района	География.	Состав: Алтайский край. Кемеровская, Новосибирская, Омская, Томская, Тюменская области, Ханты-Мансийский и Ямало-Ненецкий автономный округ. Республика Алтай.
Восточно-Сибирский экономический район	География.	Состав: (10 субъектов федерации) — Республики Бурятия, Тува (Тыва), Хакасия, Красноярский край, Иркутская и Читинская обл... Таймырский (Долгано-Ненецкий) АО, Эвенкийский АО, Усть-Ордынский Бурятский АО, Агинский Бурятский АО.
Развитие Восточно-Сибирского района	География.	Состав: Иркутская область, Читинская область, Красноярский край, Агинский Бурятский, Таймырский (Долгано-Ненецкий), Усть-Ордынский, Бурятский и Эвенкийский автономные округа. Республики: Бурятия, Тува (Тыва) и Хакасия.
Дальневосточный экономический район	География.	Состав района: (10 субъектов федерации) — Республика Саха (Якутия), Хабаровский край, Приморский край, Магаданская обл., Камчатская обл... Амурская обл., Сахалинская обл., Еврейская автономная обл., Чукотский АО, Корякский АО.
Развитие Дальневосточного экономического района	География.	Состав: Амурская, Камчатская. Магаданская, Сахалинская области, Приморский и Хабаровский края. Республика Саха (Якутия), Еврейская автономная область. Чукотский и Корякский автономные округа.
Хозяйство стран Ближнего зарубежья:
Хозяйство стран Ближнего зарубежья. Белоруссия	География.	Среди стран Ближнего зарубежья можно выделить несколько групп, отличающихся по направлению формирующейся национальной экономики.
Республики Прибалтики	География.	К прибалтийским республикам относят две граничащие непосредственно с основной российской территорией Эстонию t Латвию, а также Литву, которая имеет границу только с Калининградской областью.
Украина	География.	Украина — юго-западный сосед России, с протяженной границей, проходящей в основном по равнинной местности.
Закавказье	География.	К закавказским республикам СНГ относят две пограничные с Россией Азербайджан и Грузию, а также Армению, которые в советский период составляли один Закавказский экономический район.
Казахстан	География.	Казахстан имеет самую длинную границу с Россией — 7 тыс. км. Площадь республики Казахстан— 2717,3тыс. км2, население — 14,8 млн чел.
Средняя Азия	География.	В СССР Средняя Азия выделялась ка. самостоятельный экономический район в составе четырех республик: Узбекистан Киргизия, Туркмения и Таджикистан. Сейчас в мировой географической литературе чаще всего употребляется термин Центральная Азия, в которую входит еще и Казахстан.
Молдавия	География.	Молдавия, или Республика Молдова — одно из самых маленьких государств СНГ.

Шпаргалки (шпора) по Истории России.

История России:
Древние славяне	История России.	В римских источниках I-II вв. (Тацит, Плиний) славян называют венедами. Впервые под своим именем славяне упоминаются в VI в. у Прокопия Кеса-рийского и Иордана.
Возникновение и развитие Древнерусского государства (IX-начало XII в.)	История России.	В IX в. у славян было 2 крупных объединения. У полян в среднем Поднепровье с центром в Киеве. У словен в Поволховье с центром в Ладоге.
Политическая раздробленность на Руси (XII — XIII вв.)	История России.	В 30-40-х гг. XII в. князья перестают признавать власть киевского князя. Русь распадается на отдельные княжества («земли»). За Киев началась борьба разных княжеских ветвей.
Культура Руси в X-XIII вв.	История России.	Важную роль сыграло в развитии культуры принятие христианства. Усилились культурные связи с Византией. Возникли церковные школы и монастыри. В живопись проникают греческие каноны.
Борьба Руси против иноземных нашествий в XIII в.	История России.	В 1206 г. образовалась монгольская империя во главе сТемучином (Чингисханом). Монголы разгромили Приморье, Северный Китай, Среднюю Азию, Закавказье, напали на половцев.
Русь под игом	История России.	В 1243 г. великий хан сделал старшим среди русских князей Ярослава Всеволодовича Владимирского. После его смерти в 1246 г. началась борьба за владимирский стол, в которую вмешались ордынцы, разорившие Суздальскую землю.
Образование Русского централизованного государства	История России.	Централизованное государство возникает при Иване III (1462—1505). При нем к Москве были присоединены Ярославль, Ростов, Новгород, Тверь, Вятка. Иван III перестал платить дань Большой Орде (наиболее крупной части распавшейся Золотой Орды).
Россия при Иване IV (1533—1584 гг.)	История России.	Иван IV стал великим князем в 1533 г. в 3 года. Регентшей была его мать Елена Глинская, а после ее смерти в 1538 г. началось боярское правление, сопровождавшееся борьбой боярских группировок. В 1547 г.
Основные направления внешней политики России и рост ее территории в XV-XVI вв.	История России.	Основными направлениями внешней политики были восточное (Орда), южное (Крым и Астрахань) и западное (Литва, Швеция, Ливония).
Русская культура в XIV-XVI вв.	История России.	В XIV в. начинается новый подъем русской культуры. Идет активное каменное строительство в Москве (белокаменный кремль), Новгороде (церкви Фёдора Стра-тнпата, Петра и Павла на Славне). Создается Лаврентьевская летопись.
Смута в России	История России.	В 1598 г. умер Фёдор Иванович — последний потомок Ивана Калиты на московском троне. Его брат царевич Дмитрий погиб еще в 1591 г. в Угличе, в чём некоторые обвиняли Бориса. Династия прервалась.
Россия в XVII в.	История России.	При Михаиле Фёдоровиче (1613—1645) часто собирались Земские соборы, новая династия искала поддержки у общества. При Алексее Михайловиче (1645—1676) после 1653 г. Земские соборы уже не созывались.
Социальные движения в XVII в. Церковный раскол	История России.	XVII в. называют «бунташным» из-за серии восстаний, вызванных закрепощением, малым престижем новой династии, ростом повинностей. В 1648 г. в Москве вспыхнул «соляной бунт» из-за налогов на соль.
Реформы Петра I	История России.	Цели реформ Петра I (1682—1725) — максимальное усиление власти царя, рост военной мощи страны, территориальное расширение державы и выход к морю. Виднейшие сподвижники Петра I — А. Д. Меншиков, Г. И. Головкин, Ф. М. Апраксин, П. И. Ягужинский.
Дворцовые перевороты	История России.	После смерти Петра I часть придворных и гвардия совершили дворцовый переворот в пользу его вдовы Екатерины I. При ней фактически правил А.Д. Меншиков. Был создан Верховный тайный совет, чтобы разгрузить от лишних дел сенат.
Внешняя политика России в конце XVII в. -1-й половине XVIII в.	История России.	В 1686 г. Россия по Вечному миру с Польшей закрепила за собою Киев и вступила антитурецкую коалицию. В 1687 и 1689 гг. В. В. Голицын дважды ходил на Крым, но не достиг его. В 1695—1696 гг.
Россия при Екатерине II: просвещенный абсолютизм	История России.	Время Екатерины II (1762—1796) — «золотой век» дворянства. Его привилегии и влияние достигают апогея — царица, пришедшая к власти незаконно, нуждалась в его поддержке.
Культура и общественная мысль России в XVIII в.	История России.	При Петре I в культуру и быт активно проникают западные веяния. Это приводит к плодотворному синтезу. Основным художественным направлением в эпоху Петра был классицизм.
Внешняя политика России во 2-й пол. XVIII в.	История России.	В период правления Елизаветы в 1756 г. Россия вступила в Семилетнюю войну на стороне Австрии и Франции против опасно усилившейся Пруссии. Русские войска захватили Восточную Пруссию, в 1759 г.
Реформы Александра I	История России.	Правление Александра I ознаменовалось либерализацией самодержавия в духе просвещенного абсолютизма (амнистия пострадавших при Павле, ослабление цензуры). «Штаб» реформ с 1801 г. — неофициальный Негласный комитет (А. А. Чарторыйский, Н. Н. Новосильцев, П. А. Строганов, В. П. Кочубей).
Отечественная война 1812 г. и заграничные походы русской армии	История России.	В 1804 г. Россия, не желая чрезмерного усиления Наполеона, вновь вступила в антифранцузскую коалицию (с Австрией и Англией, в 1806 г. —с Пруссией). Но в 1805 г. ее армия была разбита под Аустерлицем, в 1807 г. — под Фридландом.
Социально-экономическое развитие России, Западной Европы и США в 1-й половине XIX в.	История России.	К XIX в. Россия обладала огромной территорией, но имела слабую плотность населения. Основу экономики составляло сельское хозяйство, промышленность была развита по сравнению с Европой и США слабо, невелика роль свободного труда.
Внутренняя политика Николая I	История России.	При Николае I (1825—1855) заканчивается эпоха «просвещенного абсолютизма». Начинается наступление на политические, а отчасти и экономические права дворянства ради укрепления самодержавия.
Общественное движение в 1-й половине XIX в.	История России.	Отечественная война 1812 г. вызвала рост патриотизма и общественного самосознания. Одна часть дворянства мечтала о введении конституции, другая говорила, кроме того, о необходимости отмены крепостного права.
Культура России в 1-й пол. XIX в.	История России.	Данный период — «золотой век» русской культуры, обусловленный творческим осмыслением западной культуры и духовным климатом времен «просвещенного абсолютизма».
Внешняя политика Николая I	История России.	1826—1828 гг. началась русско-иранская война, в результате которой Россия присоединила Армению. В 1827г. Россия вмешалась в борьбу Греции против турок за независимость, что привело к русско-турецкой войне (1828—1829).
Промышленный переворот в России в XIX в.	История России.	Промышленный переворот, т. е. переход от мануфактурного производства к машинному, начинается в 1830-х гг. и в основных отраслях завершился в 1880-х гг.
Либеральные реформы 1860—1870-х гг.	История России.	После Крымской войны отсталость России стала очевидной всем — крепостничество не обеспечивало необходимых темпов развития. В1856 г. началась подготовка его отмены, которая носила гласный характер.
Общественное движение в России во 2-й пол. XIX в.	История России.	Ослабление цензуры и репрессий при Александре II привело к росту общественного движения. В нем активно участвовали как дворяне, так и разночинная интеллигенция.
Российская империя в XIX в.: национальная политика самодержавия	История России.	В XIX в. Россия расширилась за счет включения в ее состав инонациональных территорий — Финляндии (1809), большей части Польши (1815), Азербайджана (1813), Армении (1828), Средней Азии (1864—1884) и др.
Внешняя политика России во 2-й пол. XIX в.	История России.	После Крымской войны Россия оказалась в политической изоляции. В условиях польского восстания России помогла Пруссия, сама затем получившая от нее политическую поддержку в войнах с Австрией и Францией.
Россия в царствование Александра III	История России.	Александр III (1881—1894) расправился с народовольцами, участвовавшими в убийстве его отца, отправил в отставку либеральных министров Александра II (Д. А. Милютина, М. Т. Лорис-Меликова).
Русская культура 2-й пол. XIX в.	История России.	Образование. При Александре II созданы женские гимназии и женские курсы с университетской программой. Университеты вновь получили автономию. Созданы земские училища.
Экономика и социально-политическое положение России в начале XX в.	История России.	В начале XX в. Россия была активно развивающейся страной, но с преобладанием сельского хозяйства и слабою урбанизацией. Крестьянство страдало от малоземелья и низкого уровня агротехники.
Внешняя политика России в конце XIX-начале XX в. Русско-японская война	История России.	В 1899 г. по инициативе Николая II состоялась Гаагская конференция по вопросам разоружения. Было решено запретить использование удушливых газов и разрывных пуль, создан Международный суд в Гааге.
Революция 1905—1907 гг. и ее итоги	История России.	8 начале XX в. Россия входила в число пяти крупнейших промышленных держав мира, но почти все слои русского общества были недовольны своим положением. Интеллигенция и часть дворянства желала введения конституции.
Реформы П. А. Столыпина	История России.	В связи с обострением аграрного вопроса в ходе революции правительство попыталось принять меры по его решению. Не желая отдавать крестьянам помещичью землю, оно попыталось улучшить положение крестьян другими методами.
Культура России в начале XX в.	История России.	Данный период называют «серебряным веком» русской культуры», т. к. он характеризовался новым расцветом поэзии, музыки, театра, живописи и архитектуры. Наука. В. И. Вернадский создал учение о биосфере.
Россия в Первой мировой войне 1914—1918 гг.	История России.	В 1907 г. Россия вступила в союз Англии и Франции (Антанта) против Германии и Австро-Венгрии, к которым позднее присоединились Турция и Болгария (Четверной союз).
1917 год в России	История России.	В феврале 1917 г. началась революция в Петрограде. Войска перешли на сторону народа. 2 марта Николай II отрёкся от престола.
Гражданская война в России (1918—1921)	История России.	Большевики вызвали всеобщее недовольство: у буржуазии отбирали предприятия и деньги, у дворян землю, у крестьян — излишки хлеба. Начался голод. Большевики начали политику военного коммунизма (продразвёрстка, всеобщая трудовая повинность, почти полная ликвидация торговли и др.).
Новая экономическая политика	История России.	В условиях голода, разрухи, народных восстаний в марте 1921 г. X съезд РКП(б) принял решение о прекращении политики военного коммунизма с его жёстким централизованным руководством экономикой и начале новой экономической политике (нэп).
Образование СССР	История России.	В 1917—1918 гг. Российская империя распалась. Из ее состава вышли Польша, Финляндия, Украина и др. Россия стала называться РСФСР. Однако в ходе гражданской войны пошли обратные процессы — большевики национальных окраин начали объединяться с российскими для борьбы со своими врагами.
Формирование тоталитарной системы в СССР в 20-30-е гг.	История России.	В 1921 г. X съезд партии запретил создание фракций внутри партии, чтобы избежать ее раскола (резолюция «О единстве партии»). В 1924 г. умер Ленин. Началась борьба за власть между его преемниками, и до конца 20-х гг.
Коллективизация в СССР	История России.	В 1927 г. XV съезд партии принял решение о проведении коллективизации. Ее начало подхлестнули трудности с хлебом в 1928 г. Введение коллективных хозяйств (колхозов) упростило принудительный сбор зерна с крестьян.
Индустриализация в СССР	История России.	Решение об индустриализации было принято в 1925 г. на XIV съезде партии. Ее задача — сделать СССР независимой в промышленном отношении страной и позволить ему на равных противостоять западным капиталистическим державам.
Внешняя политика СССР в 20-30-е гг.	История России.	После 1917 г. Россия оказалась в международной изоляции, ибо досрочно вышла из войны и отказалась платить царские долги. Первый договор заключила с ней, тем самым признавая, Эстония.
Культура в СССР в 20-30-е гг.	История России.	Революция и гражданская война нанесли огромный ущерб культуре — погибли или эмигрировали тысячи деятелей культуры и просто образованных людей. Общий культурный уровень понизился.
СССР в канун Великой Отечественной войны	История России.	1 сентября 1939г. войска гитлеровской Германии напали на Польшу. 3 сентября 1939 г. Англия и Франция объявили войну Германии. Началась Вторая мировая война.
Начальный период Великой Отечественной войны	История России.	22 июня 1941 г. Германия и некоторые ее союзники (Италия, Венгрия, Румыния, Финляндия) внезапно напали на СССР. Немецкие войска окружили советские части под Минском и Белостоком, заняли Белоруссию, Литву, Латвию, часть Украины.
Перелом в ходе Великой Отечественной войны	История России.	19 ноября 1942 г. Красная Армия перешла в наступление под Сталинградом и окружила группировку Ф. Пау-люса. Попытка деблокировать ее провалилась. 2 февраля 1943 г. после тяжелых боев ее остатки сдались бойцам К. К. Рокоссовского.
Завершающий этап Великой Отечественной войны	История России.	В январе 1944 г. войска И. С. Конева окружили и разгромили немцев под Корсунь-Шевченковским. Армии Л. А. Говорова и К. А. Мерецкова сняли осаду с Ленинграда. Весной освобождены Южная Украина и Крым.
СССР в 1945—1953 гг.	История России.	После войны сталинский режим достиг апогея. В годы война укрепилась национальная идея (прежде была идея мировой революции). В связи с усилившимся влиянием Запада началась борьба с «космополитизмом».
СССР в годы оттепели	История России.	Внутренняя политика. После смерти Сталина в 1953 г. началась борьба за власть. Был расстрелян Берия — глава карательных органов, которого давно боялись и ненавидели. ЦК КПСС возглавил Н. С. Хрущёв, правительство — Г.М.Маленков.
СССР в 1964—1985 гг.	История России.	После смещения Н. С. Хрущева страной последовательно руководили: в 1964—1982 гг. Генеральный секретарь ЦК КПСС Л. И. Брежнев, в 1982—1984 гг. — Ю. В. Андропов, 1984—1985 гг. — К. У. Черненко.
Внешняя политика СССР в 1964 г.	История России.	СССР продолжал политику расширения сферы влияния, поддерживая врагов США («холодная война»). Однако навязывание многим странам Азии и Африки социалистических порядков мешало внешней политике, ибо эти порядки вели к ухудшению в экономике и вызывали недовольство населения.
Культура СССР в 1964—1985 гг.	История России.	В культуре еще сохранялось какое-то время вольнодумство хрущёвской эпохи (был опубликован роман М. А. Булгакова «Мастер и Маргарита»), но постепенно оно придавливалось властями.
Правозащитное движение в СССР в 60-80-е гг.	История России.	Правозащитное («диссидентское») движение зародилось еще в 50-х гг., но оформилось лишь в 60-х гг. Крушение сталинизма побудило людей к переосмыслению действительности, многие понимали, что дело не только в Сталине, но и а коренных пороках советского строя как такового.
Перестройка в СССР	История России.	К середине 80-х гг. отставание СССР от Запада становилось всё более очевидным. Стране требовались реформы.
Распад СССР	История России.	С началом перестройки оживились оппозиционные движения в союзных республиках, особенно активные в Прибалтике и на Кавказе. Уже в 1986 г. произошли беспорядки в Алма-Ате из-за смещения местного руководителя Д. А. Кунаева и замены его русским.
Современное социально-политическое развитие России	История России.	Первым президентом России был избран в 1991 г. Б. Н. Ельцин, вице-президентом — А. В. Руцкой. Сохранялись съезд народных депутатов (формально высшая власть в стране) и Верховный Совет РСФСР (председатель — Р. И. Хасбулатов).
Россия в системе современных международных отношений	История России.	На месте СССР образовался СНГ — Союз независимых государств, куда вошли 11 республик бывшего СССР (кроме стран Прибалтики и Молдавии). Структура СНГ является весьма непрочной, фактически каждая республика, входящая в него, ведёт самостоятельную политику.

Шпаргалки (шпора) по Обществознанию.

Сочинения:
Глобальные проблемы современности и пути их разрешения	Обществознание.	К глобальным проблемам человечества относятся проблемы, затрагивающие жизненные интересы всех представителей мирового сообщества и, следовательно,требующие согласованных международных действий для их решения.
Деятельность и общение	Обществознание.	В современном научном знании вопрос о соотношения деятельности и общения остается не вполне решенным. В ряде обществоведческих теорий существует тенденция к противопоставлению общения и деятельности.
Духовная сфера общества. Проблемы развития духовной культуры современной России	Обществознание.	Духовная сфера общества — это система отношений между людьми, отражающая духовно-нравственную жизнь общества, представленную такими подсистемами, как культура, наука, религия, мораль, идеология, искусство.
Духовное производство и духовное потребление	Обществознание.	Духовное производство — это деятельность людей, направленная на создание новых духовных ценностей. Духовное производство осуществляется как особыми профессиональными группами людей (ученые, писатели, поэты, скульпторы, художники, кинорежиссеры).
Духовный мир личности. Мировоззрение	Обществознание.	Термином мировоззрение обозначается сложная система взглядов человека на мир, которые разделяются членами его социальной группы (поколения, страны, социального класса, религиозной общины и т.д.).
Исторический процесс и его участники	Обществознание.	Исторический процесс — это последовательная череда сменяющих друг друга событий, в которых проявляется деятельность многих поколений людей.
Наука и общество	Обществознание.	Чрезвычайная многоаспектность науки как социального феномена затрудняет выработку определения, которое всесторонне отражало бы его сущность.
Научное познание. Значение научной теории	Обществознание.	Научное познание имеет ряд принципиальных особенностей, отличий от знания, получаемого в сфере обыденного, стихийно-эмпирического познания. Именно эти отличия определяют преимущества науки, научного знания.
Образование и его роль в развитии общества	Обществознание.	Образование является частью процесса социализации личности, представляя собой формализованную целенаправленную передачу накопленного опыта,знаний последующим поколениям, который осуществляется в рамках соответствующих социальных институтов.
Общество и научно-технический прогресс	Обществознание.	Научно-технический прогресс (НТП) — это взаимообусловленное, поступательное развитие науки и техники, производства и сферы потребления. Научный и технический прогресс впервые стал сближаться в XVI-XVIII вв.
Особенности социального познания, конкретно-исторический подход к социальным явлениям	Обществознание.	Термин «социальное познание» интерпретируется как познание общества, социальных явлений и процессов, протекающих в нем. В этом мысле социальное познание отличается от познания других (не социальных) объектов и имеет следующие особенности.
Познание. Истина и ее критерии	Обществознание.	Для ориентации человека в окружающем мире, для интерпретации х прогнозирования событий, для планирования и реализации дея-гельности коллективов людей, для выработки новых научных представлений необходимы знания.
Понятие общества. Сферы общественной жизни	Обществознание.	В настоящее время наиболее распространенной и научно обоснованной является точка зрения, согласно которой общество рассматривася как сложноорганизованная система, обладающая наивысшим уровнем самодостаточности.
Прогресс и регресс. Критерии прогресса	Обществознание.	Прогресс — направление развития сложных систем (в том числе социальных), для которого характерен переход от низших, менее совершенных форм к высшим, более совершенным.
Развитие знаний об обществе. Общественные науки	Обществознание.	В научном знании выделяют естественные и общественные науки. Естественные науки (или как говорят — естествознание) представляют собой сумму знаний о законах и закономерностях бытия природы в целом, природных явлений в особенности.
Религия, ее место в системе отношений человека и окружающего мира. Атеизм	Обществознание.	Религия — это мировоззрение и поведение отдельного индивида, группы, общности, которые определяются верой в существование сверхъестественного.
Роль искусства в познании мира. Новаторство и традиции в культуре	Обществознание.	Искусство является особым способом познания и отражения действительности посредством художественных образов. Оно представлено в художественной деятельности человека, призванной удовлетворять потребности людей в наслаждении красотой.
Свобода в деятельности человека	Обществознание.	Проблема свободы личности — одна из актуальных проблем современности. Однако попытки ее решения осуществлялись на всем протяжении развития философской мысли.
Социальная структура. Тенденции изменения социальной структуры российского общества	Обществознание.	Общенаучное понятие «структура» (отлат. structure) интерпретируется как совокупность функционально связанных между собой элементов, составляющих внутреннее строение объекта.
Социальные нормы и отклоняющееся поведение	Обществознание.	Главным инструментом установления и поддержания порядка в обществе, стабилизации его социальных структур является социальный контроль, представляющий собой совокупность средств, с помощью которых общество регулирует поведение своих членов, делает его социально полезным и предсказуемым.
Социальный статус личности. Социальные роли личности	Обществознание.	Для анализа степени включения индивида в различные группы, а также для оценки того положения, которое он занимает в них, его функциональных возможностей по отношению к каждой группе, используются понятия «социальный статус» и «социальная роль».
Традиционное и индустриальное общество	Обществознание.	Все многообразие обществ, существовавших прежде и существующих сейчас, обществоведы разделяют на определенные типы. Существует множество способов классификации обществ.
Трудовая деятельность человека	Обществознание.	Основным исторически первичным видом человеческой деятельности является труд. Труд характеризуется как сознательная целенаправленная деятельность человека, результат которой содержится в его представлении и регулируется волей в соответствии с поставленной целью.
Целостность современного мира и его противоречия	Обществознание.	На современной фазе всемирно-исторического процесса интенсивно происходит интернационализация общественной жизни. Эта тенденция усиливает актуальность социально-философского вопроса о единстве человечества.
Цивилизации и формации	Обществознание.	В истории социально-философской мысли в рамках рассмотрения единства и многообразия истории выделяются и иногда пересекаются два основных подхода: формационный и цивилизационный.
Человек, индивид, личность	Обществознание.	Все люди, живущие на Земле уже более 50 тысяч лет, относятся к одному и тому же виду — Homo sapiens (человек разумный). Этот факт общепризнан. Однако оказалось не так просто выделить то специфическое, что отличает человека от животных.
Человеческая деятельность и ее многообразие	Обществознание.	Со второй половины XIX века, когда было признано, что человек — продукт биологической эволюции, центральным для всей теории развития человека как живого существа стал вопрос об основном отличии людей от высокоорганизованных животных и о научном объяснении этого отличия.
Политико правовая сфера жизни общества:
Государство, его признаки	Обществознание.	Государство — организация (оружие, машина) непосредственного олитического властвования. Все ругие организации, входящие в политическую систему общества, участвуют в осуществлении власти посредованно,через государство, различной мере и различных формax сотрудничая с ним.
Демократия, ее характеристика. Демократическая политическая культура	Обществознание.	Демократия — власть народа, народовластие. Демократия — многоплановое явление,которое в политологии рассматривается как.
Национальные отношения в современном мире. Проблемы межнациональных отношений в нашей стране	Обществознание.	В многонациональном государстве составной частью политических отношений являются межнациональные отношения. Государство налаживает, регулирует отношения между нациями и народностями.
Парламентаризм. Федеральное Собрание Российской Федерации	Обществознание.	Парламентаризм — система государственной власти, при которой четко распределены функции законодательных и исполнительных органов при решающей роли парламента.
Политика, ее субъекты и объекты, цели и средства	Обществознание.	«Политика — это искусство жить вместе» (Платон). Политика есть такая сфера взаимоотношений между людьми, которая касается, главным образом, проблем деятельности власти и управления.
Политическая система общества, ее структура	Обществознание.	Политическая система общества (ПСО) — целостная, упорядоченная совокупность политических институтов, политических ролей, отношений, процессов, принципов.
Политический плюрализм. Становление многопартийности в России	Обществознание.	Политический плюрализм — принцип общественно-политического и социального развития, базирующийся на существовании нескольких (или множества) независимых политических знаний.
Политический статус личности	Обществознание.	Личность является первичным субъектом политики. Как политический субъект, она характеризуется возможностью и степенью влияния на политические процессы в обществе, и главным образом на политическую власть.
Права человека. Их закрепление в Конституции РФ	Обществознание.	10 декабря 1948г. Генеральная Ассамблея Организации Объединенных Наций (ООН) приняла «Всеобщую Декларацию прав человека», которая имела международное значение, провозглашала принципы правового положения личности и носила рекомендательный характер.
Правовое государство	Обществознание.	Правовое государство — это государство, ограниченное в своих действиях правом, защищающим свободу и другие права личности, и подчиняющее власть воле суверенного народа.
Экономическая сфера жизни общества:
Государство и экономика	Обществознание.	Формы организации хозяйственной деятельности людей называют экономическими системами, кото-эые отражают отношения между экономическими субъектами по поводу производства, распределения, обмена и потребления экономических благ.
Россия на пути к рыночной экономике	Обществознание.	С разрушением командной централизованной экономики во второй половине 1980-х гг. Россия вступила на путь реформ, направленных на вхождение в рыночную экономику.
Рыночные отношения в современной экономике	Обществознание.	Рыночная экономика, основанная на принципах свободного предпринимательства, многообразия форм собственности на средства производства, рыночного ценообразования, конкуренции и ограниченного вмешательства государства в деятельность предприятий.
Человек в системе рыночных отношений	Обществознание.	Без людей не может быть никакой экономики. Экономика возникла вместе с человеком и развивается для человека, оказывая влияние на развитие человеческой личности.
Экономическая сфера общества. Структура отношений собственности в современной экономике	Обществознание.	Экономическая сфера общества — система экономических отношений, возникающая и воспроизводимая в процессе материального производства. Основой экономических отношений и главнейшим фактором, определяющим их специфику, является способ производства и распределения материальных благ в обществе.

Шпаргалки (шпора) по Философии.

Философия:
Мифология как исторический тип мировоззрения. От мифологии к философии	Философия.	Исходной для человеческого общества системой общих знаний о мире была мифология. Мифология — способ понимания и освоения природной и социальной действительности на ранних стадиях общественного развития.
Человек в философии и культуре Древнего Востока	Философия.	Восточная философская мысль менее категорична и в этом смысле более неопределенна, чем западная. Это не случайно, ибо в культуре Востока, например в Индии, используется логика, в которой нет «закона исключенного третьего».
Основные принципы философского мышления в Древней Индии	Философия.	Главная целью индийской философии — достижение вечного блаженства как до, так и после смерти. Это означает полное и вечное освобождение от всякого зла. Методом достижения этой цели выступает уход в себя, самоуглубление.
Место социально-нравственной проблематики в философии Древнего Китая	Философия.	Осознание человеком Востока себя и мира начинается, как и везде, с мифологии, которая выступает как предфи-лософский этап развития культуры. В Китае формирование предфилософско-мифологических представлений прослеживается вплоть до XVIII в. до н.э.
Космоцентризм античной философии	Философия.	Космоцентризм — это первый этап развития античной философии, который часто называют досократовским, он сохраняет вначале черты мифологии.
Основные этапы развития античной философии	Философия.	Античная философия имеет свои временные и пространственные границы. Время ее бытия — с VI в. до н.э. и до VI в. н.э., когда император Юстиниан эакрып в 529 г. н.э. последнюю философскую школу — Платоновскую Академию.
Поиск первоосновы мира в античной философии	Философия.	Родина философии в собственно европейском смысле слова — Древняя Греция.
Атомистическое учение Демокрита	Философия.	Предпосылкой атомизма была потребность дать материальное объяснение наблюдаемых свойств вещей — их множества, движения и изменения.
Суть принципа софистов: «Человек есть мера всех вещей»	Философия.	Софистика — открытый рационалистический (ранее натуралистический) период греческой философии.
Философия Сократа	Философия.	Поворотным пунктом в развитии античной философии явились воззрения Сократа (469-399 до н.э.). Его имя стало нарицательным и служит для выражения идеи лудрости.
Учение Платона об «идее»	Философия.	Платон (427-347 до н.э.) — великий мыслитель, ронизывающий своими тончайшими духовными нитями сю мировую философскую культуру.
Философия Аристотеля как энциклопедическое учение	Философия.	Философская мысль Древней Греции достигла наибольшей высоты в творениях Аристотеля (384-322 до н.э.), воззрения которого, энциклопедически вобравшие в себя достижения античной науки.
Роль философских и нравственных идей Библии в развитии мировой духовной культуры	Философия.	В Библии содержатся асе принципы, которым необходимо следовать, чтобы быть приспособленным к этой жизни и к жизни вечной.
Теоцентризм средневековой философии	Философия.	В основе средневекового человекознания лежали религиозные (теоцентристские) о своей сути установки о том, что Бог — начало всего сущего. Он создал мир, человека, определил нормы человеческого поведения.
Спор между номиналистами и реалистами в средневековой философии	Философия.	В XI веке развернулась борьба между номинализмом и реализмом. Конфликт был связан с догматом христианской религии о триединой сущности Бога. Бог един, но триедин в лицах: Бог-Отец. Бог-Сын и Бог-Святой Дух.
Патристика: суть учения и основные представители	Философия.	Средние века, охватывающие почти тысячелетие (с V по XV в.), мировоззренчески пронизаны христианскими представлениями о сущем. В IV в.
Схоластика и её роль в философии Средневековья	Философия.	Само слово «схоластика» было изобретено гуманистическими писателями, стремившимися дискредитировать идеи средневекового периода, чтобы придать еще большую привлекательность своему обращению к классическому периоду.
Антропоцентризм философии эпохи Возрождения	Философия.	Возрождение — философские и социологические учения в эпоху становления раннего буржуазного общества (в основном в Италии) 14-17вв.
Идеи гуманизма и натурфилософии в эпоху Возрождения	Философия.	Гуманизм — центральное для эпохи Возрождения культурное явление. Это свободомыслие и светский индивидуализм. Он зарождался на кафедрах университетов.
Реформация и её влияние на становление нового философского мышления	Философия.	Реформация — общественное движение в Западной и Центральной Европе XVI в. Носило в основном антифеодальный характер, приняло форму борьбы против Католической церкви. Началу Реформации послужило выступление в 1517 г. в Германии М. Лютера.
Научная революция XVII века и её воздействие на философию	Философия.	Символами общественного прогресса в XVII веке становятся первые буржуазные резолюции в Нидерландах (конец XVI — начало XVII вв.) и Англии (середина XVII в.).
Учения Ф. Бэкона и Р. Декарта: общее и различное	Философия.	Наступившее после Возрождения Новое время продолжило формировать иное отношение к природе и духовному миру человека.
Монизм, дуализм, плюрализм в философии XVII века	Философия.	Философия, обобщая наблюдение и изучение мира, неизбежно останавливается перед проблемой: сколько существует глубинных основ (начал, первопричин, исходных принципов) самою мира — один, два или больше.
Философские идеалы эпохи Просвещения	Философия.	Просвещение входит в культуру как торжество рационализма, завершение идей, которые появились в период Возрождения и получили дальнейшее развитие в XVII—XVIII вв.
Теория познания И. Канта: основные понятия и принципы	Философия.	Одним из величайших умов человечества, основоположником немецкой классической философии является Иммануил Кант (1724—1804). Не только в философии, но и 8 конкретной науке Кант был глубоким, проницательным мыслителем.
«Категорический императив» И. Канта	Философия.	Кант отрицательно относился к мнимой морали, основанной на принципах полезности и приятности, на инстинкте, внешнем авторитете и на различного рода чувствах. Ни благоразумие, ни умение еще не составляют нравственности.
Соотношение системы и метода в философии Гегеля	Философия.	Георг Вильгельм Фридрих Гегель (1770—1831) глубоко и всесторонне переработал идеи своих предшественников и создал целостную систему идеалистической диалектики.
Принцип историзма, разработанный в немецкой классической философии	Философия.	Термин «историчность» впервые появился в немецкой философской литературе более 180 лет назад, но его нельзя отнести к числу тех понятий, без которых не может обойтись ни один словарь по философии.
Суть антропологического принципа в философии Л. Фейербаха	Философия.	Видным представителем младогегельянской школы был Людвиг Фейербах. Ядром философской концепции Фейербаха был человек, который «и есть Бог». Религия у Фейербаха — продукт человеческой фантазии.
Философская концепция Маркса	Философия.	В своей философской концепции Маркс с самого начала продолжал решать традиционную для европейской мысли проблему отчуждения человека в обществе, тде господствует частная собственность на средства производства, и искал пути преодоления этого отчуждения.
Философия позитивизма и основные этапы её развития	Философия.	Позитивизм (лат. positivus — положительный) в качестве главной проблемы рассматривает вопрос о взаимоотношении философии и науки.
Основные принципы философии прагматизма и его представители	Философия.	Прагматизм (гр. pragma—дело, действие) — название философского воззрения, которое видит наиболее яркое проявление человеческой сущности в действии, и ценность или отсутствие ценности мышления ставит в зависимость от того, является ли оно действием, жизненной практикой.
Герменевтика как философское направление	Философия.	Герменевтика (гр. hermenentike — истолкование) — искусство толкования различных текстов, символов, смыслов социокультуры.
Сциентизм и антисциентизм	Философия.	Сциентизм —концепция, заключающаяся в абсолютизации роли науки в системе культуры, в идейной жизни общества. Он начал складываться в философии конца XIX— начала XX вв., когда в связи с развитием науки был поставлен вопрос о ее роли и месте в системе культуры.
Человек в «философии жизни»	Философия.	В XIX — начала XX в. относительный универсализм сложившихся эволюционных представлений о культуре «преодолевается» появлением целого ряда философских течений и школ. «Философияжизни» (В. Дильтей, Г. Зиммель, О. Шпен-глер, X. Ортега-и-Гассет, А. Бергсон и др.).
Философские аспекты учений психоанализа и неофрейдизма	Философия.	Основателем психоанализа является австрийский ученый — психиатр Зигмунд Фрейд (1856—1939). Опираясь на свой опыт лечения и диагностики людской психики, он разработал юнцепцию бессознательных психических процессов и метизаций, перенеся их на социальные явления.
Проблема свободы в экзистенциализме	Философия.	Экзистенция — способ бытия человека. Впервые в этом значении термин экзистенция употребляется Кьеркегором.
Религиозная философия XX века	Философия.	Понимание веры и религии в либеральной теологии XIX-XX вв. было в значительной степени связано с принятыми в ней принципами критических исследований Библии, особенно Нового Завета.
Особенности развития русской философии	Философия.	В качестве самостоятельного духовного явления о русской философии может идти речь, начиная с конца XVIII — начала XIX в. В широком смысле русская философия этого периода является продуктом взаимодействия самобытных идей русского православия и воззрения французских философов эпохи Просвещения.
Значение творчества М.В. Ломоносова для русской философии	Философия.	Михаил Васильевич Ломоносов (1711—1765) — гениальный ученый-энциклопедист, обогативший своими открытиями почти все области знания, разработавший естественнонаучные проблемы и внесший огромный вклад в гуманитарные науки, в частности, в филологию, к тому же незаурядный поэт.
Философские аспекты дискуссии «западников» и «славянофилов»	Философия.	Первыми представителями «органической русской философии» были западники и славянофилы. К западникам относятся: П.Л. Чаадаев, А.Л. Герцен, Т.М. Грановский, Н.Г. Чернышевский, В.П. Боткин и др.
Философские идеи Ф. Достоевского и Л. Толстого и их влияние на духовную жизнь России	Философия.	Самобытным русским мыслителем был гениальный писатель Лев Николаевич Толстой (182&-1910). Подвергая критике общественно-политическое устройство современной ему России, Толстой уповал на нравственно-религиозный прогресс в сознании человечества.
Философская система Вл. Соловьева	Философия.	Владимир Сергеевич Соловьев (1353—1900} — выдающийся, истинно гениальный мыслитель России, поражающий многогранностью своих интересов.
«Русский космизм» как философское направление	Философия.	Из всех направлений русской философии в советский период наибольшего взлета достигла философия космизма. Её основоположниками были Вл. Вернадский и К. Циолковский.
Проблема «Запад — Россия — Восток», её философские аспекты	Философия.	Особенности нынешнего этапа развития России выдвигают на первый план изучение вопроса о том, как происходит превращение одного типа культуры в другой.
Предмет философии и основные аспекты философского знания	Философия.	Философия включает в себя учение об общих принципах бытия мироздания (онтология или метафизика), о сущности и развитии человеческого общества (социальная философия и философия истории), учение о человеке и его бытии в мире.
Мировоззрение, знание, вера	Философия.	Философия составляет теоретическую основу мировоззрения, или его теоретическое ядро, вокруг которого образовалось своего рода духовное облако обобщенных обыденных взглядов житейской мудрости, что составляет жизненно важный уровень мировоззрения.
Мифология, религия, философия о происхождении и сущности мира	Философия.	Исходной для человеческого общества системой общих знаний о мире была мифология. Мифология — способ понимания и освоения природной и социальной действительности на ранних стадиях общественного развития.
Понятия «мир», «реальность», «картина мира». Условия формирования картины мира и её изменение	Философия.	Бытие (существование) — одна из исходных категорий для научного мышления которая трактуется по разному в разное время.
Понятие идеального. Идеальное и реальное, идеальное и идеал	Философия.	Идеальное — важнейшее свойство сознания. На протяжении многих веков проблема идеального остается одной из самых актуальных и сложных в мировой философии.
Категория бытия в философии	Философия.	Бытие — предельно широкая философская категория для обозначения целостности и субстанциональности мира. В европейской культуре первые определения бытия возникли еще в Древней Греции.
Идея развития и модификация её философского воплощения	Философия.	Категорию развития обычно определяют как процесс необратимых изменений системы. Для уточнения часто добавляют, что этот процесс состоит в переходе от низшего уровня организации системы к высшему и от простого к сложному.
Пространство и время как философские категории	Философия.	Материальный мир состоит из структурных объектов, которые находятся в движении и развитии, представляющие собой процессы, которые развертываются по определенным этапам.
Закон и закономерность. Детерменизм и индетерминизм, волюнтаризм и фатализм	Философия.	Одним из проявлений всеобщей связи предметов и явлений действительности является закономерная связь между ними. Отличие закономерных связей от незакономерных состоит в том, что первые имеют отличительные признаки, а вторые таковыми не обладают.
Проблема жизни, смерти и бессмертия в духовном опыте человека	Философия.	Высшей, абсолютной ценностью является человеческая жизнь. Сущность жизни в истории человечества трактовалась по-разному: от борьбы за существование (Ч. Дарвин) и способа существования белковых тел (Ф. Энгельс) до космического процесса качественных изменений «жизненного порыва» (А. Бергсон).
Сознание и бессознательное. Сознание и язык	Философия.	Сознание — одна из форм проявления нашей души, при этом очень существенная, преисполненная глубокого содержания.
Человек как объект философского осмысления. Природное и социальное в человеке	Философия.	С одной стороны, человек — существо физическое, телесное; он обуреваем влечениями, в нем сильны бессознательные импульсы. С другой стороны, человеческая природа являет нам сознательность, разумность, способность ясного понимания и осмысливания обстоятельств.
Человек, индивид, личность. Свобода и ответственность как условия существования личности	Философия.	Индивид (от лат. individuum — неделимое) — обозначение единичного в отличие от совокупности, массы; отдельное живое существо, особь, отдельный человек — в отличие от коллектива, социальной группы, общества в целом.
Основные этапы и формы процесса познания	Философия.	Проблема познавательной деятельности человека занимает одно из очень важных мест в общей структуре философского знания. Сущность человека заключается в постоянном удовлетворении информационной, познавательной потребности, а она лежит в основе определения человеком смысла своей жизни.
Истина и заблуждения. Достоверность знания. Критерии истинности	Философия.	Обычно истину определяют как соответствие знания объекту. Истина — это адекватная информация об объекте, получаемая посредством либо чувственного или интеллектуального постижения, либо сообщения о нем и характеризуемая с точки зрения ее достоверности.
Наука, её особенности и социальные функции. Философия науки	Философия.	Наука — это деятельность человека по выработке, систематизации и проверке знаний. Научным может считаться только хорошо проверенное и обоснованное знание. Знание становится научным когда оно достигает некоторого, достаточно высокого развития, порога научности.
Методы и формы научного познания	Философия.	Метод познания можно определить как некоторую специфическую процедуру, состоящую из последовательности определенных действий или операций, применение которых либо приводит к достижению поставленной цели, либо приближает к ней.
Предсказание и прогноз. Особенности социального прогнозирования	Философия.	В ходе наблюдения и эксперимента осуществляется описание, протоколирование. Основное научное требование к описанию — его достоверность, точность воспроизведения данных наблюдений и эксперимента.
Понятия «общество» и «социальные отношения». Система социальных отношений	Философия.	Общество есть выделившаяся из природы и надстроенная над нею искусственная реальность («вторая природа»), единственно в которой возможна и реально происходит жизнеобеспечивающая деятельность вышедших из природы и неотделимых от нее людей.
Проблема типологии исторического процесса	Философия.	Философы и историки по-разному смотрят на исторический процесс. Историки подходят к изучению истории общества с позиций науки, их цель — получение достоверного, истинного знания в отношении любых конкретных, зафиксированных фактов и событий.
Культура и цивилизация: многообразие их форм, особенности	Философия.	В современном философском языке понятия «культура» и «цивилизация» — одни из самых распространенных и многозначных. Термин «культура» (лат. culture) переводится как «возделывание, обработка, развитие, почитание».
Понятие духовной жизни общества. Закономерности формирования и функционирования духовной жизни общества	Философия.	Духовная жизнь человека и человечества — феномен, который отличает их бытие от чисто природного и придает ему социальный характер. Через духовность идет осознание окружающего мира, выработка более глубокого и тонкого отношения к нему.
Техника: её специфика и закономерности развития. Техника и технические науки. Философия техники	Философия.	Под техникой понимается система созданных средств и орудий производства, а также приемы и операции, умение и искусство осуществления трудового процесса. В технике человечество аккумулировало свой многовековой опыт, приемы, методы познания и преобразования природы, воплотило все достижения человеческой культуры.
Понятие «информация». Информатизация: тенденции в изменении сознания, мышления, культуры	Философия.	Философские определения понятия «информация» отличаются чрезвычайной противоречивостью вплоть до полярности. На одном полюсе— безграничный панинформизм (удачное выражение проф. А.В. Соколова), на другом — полнейший информационный нигилизм.
Глобальные проблемы, причины их возникновения и основные признаки. Классификация глобальных проблем	Философия.	Возникновение глобальных проблем, возрастание опасности их последствий ставят новые задачи перед наукой в прогнозировании и способе их решения. Глобальные проблемы — это сложная и взаимосвязанная система, которая оказывает воздействие на общество в целом, человека и природу.
Словарь терминов	Философия.	Словарь терминов по Философии.

Шпаргалки (шпора) по Сопромату.

Сопромат:
Основные гипотезы сопротивления материалов	Сопромат.	При построении теории расчета невозможно отразить все многообразие свойств реальных материалов, поэтому приходится делать целый ряд допущений, упрощающих расчеты.
Расчетная схема	Сопромат.	В сопромате расчеты производятся с помощью расчетных схем.
Внутренние силы	Сопромат.	Между соседними частицами тела (молекулами, кристаллами, атомами) всегда имеются определенные силы взаимодействия, иначе внутренние силы.
Классификация внешних сил	Сопромат.	Внешними силами называют силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами.
Метод сечений (розу)	Сопромат.	Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию, чтобы внутренние силы стали явными.
Построение эпюр внутренних силовых факторов	Сопромат.	Задача определения наибольших напряжений начинается с поиска сечения, в котором действуют наибольшие внутренние усилия.
Эпюры внутренних усилий	Сопромат.	В случаях растяжения-сжатия (а) или кручения (б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях.
Понятие о напряжениях	Сопромат.	Брус может выдержать большую или меньшую нагрузку в зависимости от толщины или от свойств его материала. Необходимо ввести физическую величину (или характеристику), позволяющую учесть эти особенности работы конструкции под нагрузкой.
Понятия о деформациях	Сопромат.	Реальные тепа под воздействием внешних сил могут изменять свою форму и размеры, т.е. деформироваться.
Виды нагружения (или виды деформации стержня)	Сопромат.	В сопромате различают несколько простейших видов нагружения и несколько сложных. К простейшим относятся следующие.
Основные условия прочности. допускаемые напряжения. условие жесткости	Сопромат.	Ответы на вопросы о прочности может дать оценка прочности конструкции, которая сводится к сравнению расчетных напряжений с допускаемыми.
Растяжение — сжатие	Сопромат.	Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продопьная сила (растягивающая или сжимающая), а все остальные внутренние усилия равны нулю.
Напряжения и расчет на прочность	Сопромат.	При центральном растяжении (сжатии) в поперечном сечении возникают нормальные напряжения.
Деформации и перемещения при растяжении — сжатии	Сопромат.	При растяжении и сжатии бруса меняются его продольные и поперечные размеры.
Статистически неопределимые задачи	Сопромат.	Для обеспечения кинематической неизменяемости плоской упругой системы на нее должны быть наложены 3 связи.
Кручение	Сопромат.	Кручением называется такой вид деформации, при котором в поперечном сечении вала возникает только крутящий момент Мкр, а все остальные внутренние силовые факторы равны нулю.
Построение эпюр крутящих моментов	Сопромат.	Построение эпюры крутящих моментов для вала.
Напряжение и расчет на прочность	Сопромат.	Расчет стержня круглого поперечного сечения на прочность.
Геометрические характеристики плоских сечений	Сопромат.	Простейшими видами напряженного состояния стержневых элементов конструкции являются: растяжение, кручение и изгиб. Основные расчетные формулы для определения напряжений и деформаций.
Статистические моменты сечения	Сопромат.	При определении положения центра тяжести сечения необходимо определять значения статических моментов этого сечения.
Моменты инерции сечения	Сопромат.	Моменты инерции сечения входят в формулы для напряжений и деформаций.
Моменты сопротивления сечения	Сопромат.	Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию от оси до наиболее удаленной точки поперечного сечения.
Рациональные формы поперечных сечений	Сопромат.	Нормальные напряжения в произвольной точке поперечного сечения балки при прямом изгибе определяются по формуле.
Изгиб	Сопромат.	Изгиб является наиболее частым случаем на-гружения различных систем: изгиб испытывают оси транспортных средств, рельсы, детали машин, механизмов и строительных сооружений.
Напряжение при изгибе и расчет брусьев на прочность	Сопромат.	Во всех точках поперечного сечения бруса при поперечном изгибе возникают нормальные и касательные напряжения (на рис. 5.1,6 эти напряжения показаны в точках, отстоящих на расстоянии Y от оси X).
Построение эпюр изгибающих моментов	Сопромат.	Рассмотрим пример построения эпюр поперечных сил Q и изгибающих моментов Мx.
Определение перемещений в статистически определимых системах. расчеты на жесткость	Сопромат.	Одной из задач сопротивления материалов является оценка жесткости конструкции, т.е. степени ее искажения под действием нагрузки. Если балка под нагрузкой сильно прогибается, то при ее эксплуатации появятся затруднения.
Определение перемещения методом мора	Сопромат.	Существует несколько способов определения перемещений поперечных сечений при изгибе. Если не требуется знание уравнения изогнутой линии бруса, а необходимо определить только линейные или угловые перемещения отдельного сечения, удобнее всего воспользоваться методом Мора.
Правило верещагина	Сопромат.	При вычислении интегралов вместо аналитических выражений моментов используются их эпюры. Т.е. значение можно найти по способу Верещагина, «перемножив» эпюры Мp и М1.
Примеры определения перемещений при изгибе	Сопромат.	Для балки, защемленной одним концом и нагруженной на свободном конце силой Р, определить прогибы свободного конца и сечения.
Сложное нагружение	Сопромат.	Простые случаи нагружения твердого тела — растяжение, кручение и изгиб являются основой для более сложных нагружений, которые являются их комбинацией.
Косой изгиб	Сопромат.	Косым изгибом называется такой вид изгиба, при котором плоскость нагрузки (силовая линия) изгибающего момента не совпадает ни с одной из главных осей инерции поперечного сечения стержня X, Y.
Внецентренное растяжение — сжатие	Сопромат.	Внецентренным растяжением (сжатием) называется такой вид нагружения, при котором равнодействующая внешних сил не совпадает с осью стержня, как при обычном растяжении (сжатии), а смещена относительно продольной оси и остается ей параллельной.
Изгиб с кручением круглых валов	Сопромат.	Для использования основных расчетных формул, использующих эквивалентные напряжения, необходимо определить главные нормальные напряжения. (Три главные напряжения определяются кубическим уравнением, точные решения которого даются формулами Кордано).
Расчет на прочность пространственнс рамы с ломаной осью	Сопромат.	В пространственной раме, в отличие от плоской, как стержни, составляющие раму, так и нагрузки не находятся в одной плоскости (рис 7.4 а, 6). При построении эпюр используется, как и в других случаях, метод усечений.
Устойчивость сжатых стержней	Сопромат.	Исследование причин разрушения сооружений показало, что для надежной работы конструкции под нагрузкой недостаточно сделать ее элементы прочными, необходимо еще обеспечить сохранение первоначальной формы равновесия как самих элементов, так и всей конструкции в целом.
Определение критической силы по формуле эйлера	Сопромат.	Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения.
Определение критической силы с помощью эмпирической формулы	Сопромат.	Если гибкость стержня меньше предельного значения — область ВС, то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим.
Практический метод расчета на устойчивость	Сопромат.	В основу рачетов сжатых стержней на устойчивость положено требование, согласно которому допустимое напряжение должно быть меньше не только предела текучести.
Определение критической силы с помощью дифференциального уравнения (точечный метод определения ркр)	Сопромат.	Если коэффициент приведения длины не очевиден, то Ркр можно найти, решая дифференциальное уравнение — это точный метод определения критической силы.
Энергетический метод определения критической силы	Сопромат.	Ввиду трудности интегрирования дифференциального уравнения упругой линии стержня часто применяют различные приближенные методы определения критической силы.
Основные обозначения, принятые в сопромате	Сопромат.	Р — сосредоточенная сила (условно как бы приложенная в одной точке), g — интенсивность распределенной нагрузки, сила на единицу длины (Н/м, МН/м), М — внешний момент, действующий на элемент конструкции (изгибающий или крутящий) и.т.д.

Репетитор по Математике.

Репетитор по Математике:
Предисловие	Репетитор по Математике.	Для итоговой аттестации в 11 классе по курсу «Математика» (курс А) и по курсу «Алгебра и начала анализа» (курс В). Тексты заданий предполагаются открытыми для использования в обычном учебном процессе или при специальной подготовке (например, в системе экстерната). Экзаменационная работа, содержит десять заданий.
Раздел 1. Задания 1- 5 для экзаменов «Математика» и «Алгебра и начала анализа»(I)	Репетитор по Математике.	Задания 1—5 для экзаменов «Математика» и «Алгебра и начала анализа».
Раздел 1. «Математика» и «Алгебра и начала анализа» (II)	Репетитор по Математике.	«Математика» и «Алгебра и начала анализа» (II)
Раздел 1. «Математика» и «Алгебра и начала анализа»(III)	Репетитор по Математике.	«Математика» и «Алгебра и начала анализа» (III).
Раздел 2. Задания 6-7 для экзаменов «Математика»	Репетитор по Математике.	Задания 6-7 для экзаменов «Математика».
Раздел 3. Задания 8 для экзаменов «Математика»	Репетитор по Математике.	Задания 8 для экзаменов «Математика».
Раздел 4. Задания 9, 10 для экзаменов «Математика» задания 6, 7 для экзаменов «Алгебра и начала анализа»	Репетитор по Математике.	Задания 9, 10 для экзаменов «Математика» задания 6, 7 для экзаменов «Алгебра и начала анализа».
Раздел 5. Задания 8 для экзаменов «Алгебра и начала анализа»	Репетитор по Математике.	Задания 8 для экзаменов «Алгебра и начала анализа».
Раздел 6. Задания 9, 10 для экзаменов «Алгебра и начала анализа»	Репетитор по Математике.	Задания 9, 10 для экзаменов «Алгебра и начала анализа».
Вариант экзаменационного задания по курсу «Математика»	Репетитор по Математике.	Вариант экзаменационного задания по курсу «Математика».
Вариант экзаменационного задания по курсу «Алгебра и начала анализа»	Репетитор по Математике.	Вариант экзаменационного задания по курсу «Алгебра и начала анализа».
Справочный материал	Репетитор по Математике.	Справочный материал Алгебра и начала анализа.
Решения для задач Алгебра и начала анализа Алимов Ш.А. 10-11 класс.
Решение задач (I)	Репетитор по Математике.	Решение задач (I) задания.
Решение задач (II)	Репетитор по Математике.	Решение задач (II) задания.
Решение задач (III)	Репетитор по Математике.	Решение задач (III) задания.
Решение задач (IV)	Репетитор по Математике.	Решение задач (IV) задания.
Решение задач (V)	Репетитор по Математике.	Решение задач (V) задания.
Решение задач (VI)	Репетитор по Математике.	Решение задач (VI) задания.
Решение задач (VII)	Репетитор по Математике.	Решение задач (VII) задания.
Решение задач (VIII)	Репетитор по Математике.	Решение задач (VIII) задания.
Решение задач (IX)	Репетитор по Математике.	Решение задач (IX) задания.
Решение задач (X)	Репетитор по Математике.	Решение задач (X) задания.

http://vseshpargalki.narod.ru/Universalnye_shpargalki.html — link